4.22
(待补)
描述
给定两个队列$a$,$b$,每队$n$人,身高分别为$a_i$, $b_i$
每队的人都可以与前后相邻者交换位置,次数不限,仅在同队换,问使$\sum (a_i - b_i)^2$最小的交换次数
思路
两队同时换和只换一队效果相同,因此只需选一队来换。
$\sum (a_i - b_i)^2 = \sum((a_i + b_i)^2 - 4 * a_i * b_i)$
前者是定值,因此只需找到使后面那项最大的方式即可
就是求一个数列相对于另一个的逆序对(好像某次abc做过,但后来没补题…)
代码(copy的)
const int mod = 1e8 - 7;
long long n, x[10000005], p[1000005], ans = 0;
struct fire {
int hi, bh;
} l1[1000005], l2[1000005];
bool cmp1(fire a, fire b) {
return a.hi < b.hi;
}
void msort(int s, int t)//归并排序;
{
if (s == t)return;
int mid = (s + t) / 2;
msort(s, mid);
msort(mid + 1, t);
int i = s, k = s, j = mid + 1;
while (i <= mid && j <= t) {
if (x[i] <= x[j]) {
p[k] = x[i];
++k;
++i;
} else {
p[k] = x[j];
++k;
++j;
ans = (ans + mid - i + 1) % mod;
//此处找到逆序对,mid-i~mid中数全都与j构成逆序,还会少算一个,+1;
}
}
while (i <= mid) {
p[k] = x[i];
++k;
++i;
}
while (j <= t) {
p[k] = x[j];
++k;
++j;
}
for (int i = s; i <= t; i++) {
x[i] = p[i];
}
}
int main() {
scanf("%lld", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &l1[i].hi), l1[i].bh = i;
for (int i = 1; i <= n; i++)
scanf("%d", &l2[i].hi), l2[i].bh = i;
sort(l1 + 1, l1 + n + 1, cmp1);
sort(l2 + 1, l2 + n + 1, cmp1);
//排序;
for (int i = 1; i <= n; i++)
x[l2[i].bh] = l1[i].bh;
msort(1, n);
//调用归并;
printf("%lld", ans);
return 0;
}
4.23
(BFS板题)
题目描述
给出一个 N 个顶点 M 条边的无向无权图。
问从顶点 1 开始,到其他每个点的最短路有几条。
思路
BFS板题,每次遍历的时候记录层数,如果当前遍历到的$x$节点是$t$节点的下一层,那么$x$的最短路数量就是当前$x$的最短路数量加上$t$的最短路数量
因为每次遍历到的时候都会加一遍,就相当于乘法了
代码
const int N = 1e6 + 5;
const int mod = 100003;
vector<int>e[N];
int used[N];
int cnt[N];
int dep[N];
void bfs(){
queue<int>q;
dep[1] = 0;
used[1] = 1;
q.push(1), cnt[1] = 1;
while (!q.empty()){
int t = q.front();
q.pop();
for (auto x : e[t]) {
if (!used[x]){
used[x] = 1;//标记为遍历过了
dep[x] = dep[t] + 1;//层数++(因为是bfs所以层数一定是最小的)
q.push(x);
}
if (dep[x] == dep[t] + 1){//如果当前x是t的下一层
cnt[x] = (cnt[x] + cnt[t]) % mod;//那么x的最短路数量再加上t的最短路数量(每个x都加相当于乘)
}
}
}
}
void solve(){
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i++) {
int x , y;
cin >> x >> y;
e[x].push_back(y);
e[y].push_back(x);
}
bfs();
for (int i = 1; i <= n; i++) {
cout << cnt[i] << endl;
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
solve();
return 0;
}
4.26
题目链接
描述
判断有没有一种办法可以将从$1$ 到 $N$ 的 $N$个人排成一排,并满足给定的$M$个要求。
对于每个要求给出两个整数 $A_i$和$B_i$,表示编号$A_i$和$B_i$的人是相邻的
保证每个要求都不同,即给出$1$,$5$就不会再给出$5$,$1$或重复的
分析
满足题目要求的只有无环的链
即判断两件事:
1.度数是否大于等于$2$
2.是否有环
代码
const int N = 1e5 + 5;
int father[N];
int ufind(int x) {//寻找操作
if (x == father[x])
return x;
int fx = ufind(father[x]);
return father[x] = fx;
}
void solve() {
int n, m;
cin >> n >> m;
for (int i = 0; i <= n; i++) {
father[i] = i;
}
map<int, int> mp;
int ok = (n > m); // 这一点最开始没想到,如果要求大于n - 1条可以直接返回
if (!ok) {
cout << "No" << endl;
return;
}
int x, y;
for (int i = 0; ok && i < m; i++) {
cin >> x >> y;
mp[x]++;
mp[y]++;
int fx = ufind(x);
int fy = ufind(y);
if (fx != fy) {
father[fx] = y;
}
ok = (fx != fy); // 判断是否指向同一个(也包括判断环)
if (mp[x] > 2 || mp[y] > 2) // 判断度数
ok = 0;
}
cout << (ok ? "Yes" : "No") << endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
solve();
return 0;
}
好像能默写并查集中“并”的部分了= =
查的部分好像还是只能抄板子 菜菜QWQ
(突然发现图论的部分涉及的不多
4.27
题目链接
描述
现给定两个 四位素数 a,b。 你可以执行多次下面的操作:
修改数字 a 的某一位, 使其成为另一个 四位素数。
例如,1033→1733,其中 1033 与 1733 均为素数。
问至少多少次变换后能从 a 得到 b ? 或回答不可能
思路
想到了和cf某场的2B很像,只不过那场不需要按位处理,而是加1或加2后取余,做法是BFS。那这题也一样,但开始没想到怎么去枚举每一位的数字的变化,甚至想用to_string()来做,后来发现取每一位取模后除就行了…是C语言期末考试难度的题…
提醒自己多注意细节问题,多个$testcase$的时候一定要将全局变量清空!!!
更多细节见代码
代码
int prime[10000], used[10000];
int cnt[10000];
void init(){
int j;
for (int i = 1000; i <= 10000; i++) {
for (j = 2; j < i; j++) {
if (i % j == 0){
prime[i] = 0;
break;
}
}
if (j == i){
prime[i] = 1;
}
}
}
int bfs(int x, int y){
for (int i = 1000; i < 10000; i++) { // 因为忘清空WA了一次
cnt[i] = 0;
used[i] = 0;
}
queue<int>q;
int temp = 0, v[4];
q.push(x);
used[x] = 1;
cnt[x] = 0;
while (!q.empty()){
int t = q.front();
if (t == y)
return cnt[t];
q.pop();
v[0] = t / 1000;
v[1] = t % 1000 / 100;
v[2] = t % 100 / 10;
v[3] = t % 10;
for (int i = 0; i < 4; i++) {
int vtemp = v[i];
for (int j = 0; j < 10; j++) {
if (j != vtemp){
v[i] = j;
temp = 1000 * v[0] + 100 * v[1] + 10 * v[2] + v[3];
if (prime[temp] && !used[temp]){
q.push(temp);
used[temp] = 1;
cnt[temp] = cnt[t] + 1;
}
// if (temp == y)
// return cnt[temp];后来发现这步完全是多余的,因为如果是第一次到的话cnt应该是没值的
}
v[i] = vtemp; // 写的时候遗漏了这一步,在进入下一个i的循环之前要将上一次的v[i]复原
}
}
}
return -1; // 前面都没return这里只能return -1了
}
void solve(){
int n;
cin >> n;
init();
int a, b;
while (n--){
cin >> a >> b;
cout << bfs(a, b) << endl;
}
}
这种简单题以后争取十分钟以内切吧(
4.28
题目链接
描述
给定一个$H$行和$W$列的网格,我们让$(i,j)$表示从北边第i行和从西边第j列的网格
-
在一个网格上修建一个火车站的代价是$A_{i,j}$
-
在两个网格间建一条铁轨的代价是这两个点位置的曼哈顿距离
求造一条铁路的最小花费
思路
基本拿到手就是懵的,知道要用dp去做,但是完全没思路,看了题解视频好像是dp + 二维前缀和的思想去做。抄了份代码过了之后看了贴两份代码吧,之后再补(
(4.29补):
看懂思路了,分为两种情况考虑:
- 第二个点的$x$和$y$均大于第一个点,此时向第二个点的左上方扫
- 第一个点只有$x$大于第二个点,此时向第二个点的右上方扫
当然,在二维数组里面往斜上方硬扫应该是会超时的,复杂度应该是$O(n^2m^2)$
所以在第一次扫的时候要利用类似二维前缀和的思想去处理(其实感觉dp思想多一点,但是dls题解说是前缀和)
对于第一种情况,$ans$拆开来的结果是
$$A_{x2y2} + C \times (x_2 + y_2) + A_{x1y1} - C \times (x_1 + y_1)$$
当第二个点确定以后,问题就转化成求$A_{x1y1} - C \times (x_1 + y_1)$的最小值了,用$f[i][j]$去记录左上方的这个式子的最小值
可得转移方程为f[i][j] = min(f[i-1][j],f[i][j-1])
然后进行答案的更新ans = min(ans,f[i][j] + a[i][j] + c * (i + j))(注:$f[i][j]$是不包含$a[i][j]$的)
最后,已经在$a[i][j]$更新过$ans$了,那就可以把$a[i][j]$算进去了f[i][j] = min(a[i][j] - c * (i + j),f[i][j])
第二种情况往右上扫思路相同,略。
代码(copy)
/***
第一份
***/
const int N = 1005;
ll a[N][N],b[N],d[N];
void solve() {
for (ll i = 0; i < N; i++) b[i] = d[i] = 1e18;
ll n, m, c;
ll ans = 1e18;
cin >> n >> m >> c;
for (ll i = 1; i <= n; i++) {
for (ll j = m; j >= 0; j--)
d[j] = min(d[j], d[j + 1]);
for (ll j = 1; j <= m; j++) {
cin >> a[i][j];
b[j] = min(b[j], b[j - 1]);
d[j] = min(d[j], d[j + 1]);
ans = min(ans, b[j] + a[i][j] + c * i + c * j);
ans = min(ans, d[j] + a[i][j] + c * i - c * j);
b[j] = min(b[j], a[i][j] - c * i - c * j);
d[j] = min(d[j], a[i][j] - c * i + c * j);
}
}
cout << ans;
}
/***
第二份(好像还有注释 太良心了)
***/
const int N = 1100 ;
int n,m ;
int a[N][N] ;
ll f[N][N],c ;
// 其实就是找到两个点,这两个点的 C * (| x1 - x2 | + | y1 - y2 |) + a_x1_y1 + a_x2_y2
// 为了让这个值更小,我们可以使用常用的技巧将这个式子拆开
// 拆开之后看看 值有没有改变
// 发现两个点的位置会有四种关系,,如果定义一种偏序关系,那么我们就可以设定为2种关系
// 1. 第一个点完全在第二个点的下面,就是说,第一个点的 x1 和 y1 分别小于 x2,y2
// 那么拆开式子之后就是 a_x1_y1 + C * (x2 - x1 + y2 - y1) + a_x2_y2
// a_x2_y2 + C * (x2 + y2) + a_x1_y_1 - C * (x1 + y1) ;
// 为了让这个式子最小值,那么当固定了x2,那么就需要求出1这个点的 a_x1_y_1 - C * (x1 + y1) 最小值
// 如果让第一个点的 x 永远大于第二个点
// a_x1_y1 + a_x2_y2 + C * ( x1 - x2 + y2 - y1) ;
// a_x2_y2 + C * (-x2 + y2) + a_x1_y1 + c * (x1 - y1) ;
int main(){
scanf("%d%d%lld",&n,&m,&c) ;
for(int i = 1 ;i <= n ; i ++)
for(int j = 1; j <= m ; j ++)
scanf("%d",&a[i][j]) ;
ll ans = 1e18 ;
memset(f,0x3f,sizeof f) ;
for(int i = 1; i <= n ; i ++){
for(int j = 1; j <= m ; j ++){
f[i][j] = min(f[i-1][j],f[i][j-1]) ;
//cout << i << " " << j << " " << f[i][j] + a[i][j] + c * (i + j) << "\n" ;
ans = min(ans,f[i][j] + a[i][j] + c * (i + j)) ;
f[i][j] = min(a[i][j] - c * (i + j),f[i][j]) ;
}
}
memset(f,0x3f,sizeof f) ;
for(int i = 1 ; i <= n ; i++){
for(int j = m ; j >= 1 ;j --){
f[i][j] = min(f[i-1][j],f[i][j+1]) ;
//cout << i << " " << j << " " << f[i][j] << " " << a[i][j] + c * (j - i) << "\n" ;
ans = min(ans,f[i][j] + a[i][j] + c * (i - j)) ;
f[i][j] = min(a[i][j] + c * (j - i),f[i][j]) ;
}
}
printf("%lld\n",ans);
return 0 ;
}
4.29
题目链接
描述
桌子上从左到右放着 $n$ 个糖果。糖果从左到右编号,第 $i$ 块糖果的重量为 $w_i$。小明和小红要吃糖果。
小明从左边开始吃任意数量的糖果。(连续吃,不能跳过糖果)
小红从右边开始吃任意数量的糖果。(连续吃,不能跳过糖果)
当然,如果小明吃了某个糖果,小红就不能吃它(反之亦然)。
他们的目标是吃同样重量的糖果,请问此时他们总共最多能吃多少个糖果?
思路
div4的F题原题,方法是双指针,当两个指针没合到一起时分三种情况讨论:
-
当小明当前吃的重量小于小红,那么小明吃一颗,且指针向右移动一位
-
小红小于小明,小红吃一颗,指针左移一位
-
二人相等,则此时更新$ans$,$ans = max(ans, l + 1 + n - r)$
代码
void solve(){
int n;
cin >> n;
vector<int>a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
int l = -1, r = n;
ll al = 0, bo = 0;
int ans = 0;
while (l < r){
if (al < bo){
l++;
al += a[l];
}
else if (al > bo){
r--;
bo += a[r];
} else{
ans = max(ans, l + 1 + n - r);
l++;
al +=a[l];
}
}
cout << ans << endl;
}
光速下班
4.30
题目链接
描述
有一个长度为 $∑a_i$ 的木板,需要切割成 $n$ 段,每段木板的长度分别为 $a_1,a_2,…,a_n$。
每次切割,会产生大小为被切割木板长度的开销。
请你求出将此木板切割成如上 $n$ 段的最小开销。
思路
倒着考虑,每次切割会产生大小为被切割木板长度的开销 $==$ 每次合并产生合并后长度的开销
那么此时这个题就变成了非常经典的二叉堆的题目了 且一月份做过原
用优先队列,复杂度是$O(nlogn)$
优先队列还是没怎么用过,多练练吧
代码
void solve(){
int n;
cin >> n;
priority_queue<ll,vector<ll>,greater<ll>>q;
for (int i = 0; i < n; i++) {
int x;
cin >> x;
q.push(x);
}
ll ans = 0;
while (q.size() > 1){
ll t1 = q.top();
q.pop();
ll t2 = q.top();
q.pop();
q.push(t1 + t2);
ans += t1 + t2;
}
cout << ans << endl;
}
光速下班
拓展
题意完全一样,只是$n$的范围由$10^5$增加至$10^7$,$a_i$仍为$10^5$
思路
回到问题的本质,很容易想到就是排序然后选最小两堆,再把最小的那一堆插入。
但是对于$10^7$的数据,$O(nlogn)$的插入复杂度显然是不可接受的
那就需要优化插入操作的复杂度了,且将初始化的排序优化为桶排序(因为$a_i$只有$10^5$)
做法是建立两个队列,将桶排的结果放进第一个队列$Q_1$,将合并的结果放进第二个队列$Q_2$,每次取两个队列的最小值合并
(其实就是把合并的结果单独放在一个队列里面,这样就不用插入了)
复杂度为$O(n)$
代码
int cnt[100005];
queue<ll>q1;
queue<ll>q2;
ll temp;
ll get_first(){
if (q2.empty() || (!q1.empty() && q1.front() < q2.front())){
temp = q1.front();
q1.pop();
return temp;
} else{
temp = q2.front();
q2.pop();
return temp;
}
}
void solve(){
int n, x;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> x;
cnt[x]++;//准备桶排
}
for (int i = 0; i <= 100000; i++) {//WA了一发才发现最开始没挂等号...
while (cnt[i]--)
q1.push(i); //还是得多注意细心,第一次这个地方写成push(x)找了半天没发现
}
ll ans = 0;
ll a, b;
while (q1.size() + q2.size() > 1){
a = get_first();
b = get_first();
q2.push(a + b);
ans += a + b;
}
cout << ans << endl;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
solve();
return 0;
}
在洛谷原题被卡常数卡傻了,吸氧都过不去,571ms都不能过???
5.1
(待补)
题目链接
描述
给定一个长度为$n$的数组$a_1,a_2,…,a_n$。请求出下面式子模$1e9+7$的值。
$$\sum_{i = 1}^{n - 1}\sum_{j = i + 1}^{n}(a_i XOR a_j)$$
思路
待补
代码(copy)
const int mod = 1e9 + 7;
int s[2][61];
void solve(){
int n;
cin >> n;
ll ans = 0;
ll x;
for (int i = 0; i < n; i++) {
cin >> x;
for (int j = 59; j >= 0; j--) {
ll t = x >> j & 1;
ans = (ans + s[t ^ 1][j] * ((1ll << j) % mod)) % mod;
s[t][j]++;
}
}
cout << ans << endl;
}
5.2
题目链接
描述
输入正整数$k$,找到所有正整数$y\leqslant x$,使得$\dfrac{1}{k} = \dfrac{1}{x} + \dfrac{1}{y}$’
$k \leqslant 10^7$
思路
看到数据范围就知道肯定不可能$n^2$枚举,只能用$O(n)$扫一遍
通过推公式化简得: $$x = \dfrac{k \times y}{y - k}$$
而y有一个隐藏条件:因为$y\leqslant x$,所以当y等于x的时候能取到最大值,而此时$x=y=2\times k$
所以$y$的范围就限定在了$(k < y \leqslant 2\times k)$
因此只需要枚举每一个$y$,再判断$x$是否合法就行了
需要注意的细节:
1. 推出公式得到的$k \times y$在$1e7$的时候会爆int
2. 最好能不用double就不用double,判断是否为整数除了用(int)还可以分子对分母取模
3. $y$的范围是从$k + 1$开始,如果从$k$开始会出现模$0$的状况而退出程序(或返回任意值)
其实这三点就是做这个简单题踩过的坑…现在知道为什么蓝桥杯会输麻了
代码
void solve(){
int k;
cin >> k;
ll y, cnt = 0;
for(y = k + 1; y <= 2 * k; y++){
ll ok = (k * y) % (y - k);
if (!ok)
cnt++;
}
cout << cnt << endl;
}
5.3
题目链接
描述
给出一个长度为$N$的数组$A$和一个数字$k$
请问数组A中有多少个子数组,其元素和为$k$?
$1≤N≤2×10^5 ,|A_i|≤10^9,|k|≤10^{15}$
思路
首先看数据范围,因为有负数,所以双指针应该是不行的。
看到区间和首先想到的就是前缀和,遍历一遍$a_i$,每次如果找到区间和为$k$的就$cnt$++
但是如果直接硬扫的话是$O(n^2)$的,肯定不行,所以要换另一种查询的方法,可以选择set或者map(这个思想zj在某次div2B也说过)
以map为例,满足条件的前缀和和当前前缀和必定差值为$k$,只需要$O(n)$扫一遍,用map统计前缀和的出现次数然后cnt+=mp[sum - k]即可
还有就是记得mp[0]记得初始化为$1$
代码
ll get_sum(vector<int>& nums, ll k){
ll res = 0, sum = 0;
unordered_map<ll,int>mp;
mp[0] = 1;
for(auto num : nums){
sum += num;//用sum表示当前到当前数字的前缀和
if (mp[sum - k] > 0)
res += mp[sum - k];
mp[sum]++;
}
return res;
}
void solve(){
int n;
cin >> n;
ll k;
cin >> k;
vector<int>a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
cout << get_sum(a, k) << endl;
}
5.4
题目链接
描述
对于每一个长度为 $n$ 的排列 $a$,我们都可以按照下面的两种方式将它建成一个图:
1.对于每一个 $1≤i≤n$,找到一个最大的 $j$ 满足 $1≤j<i,a_j>a_i$,将 $i$ 和 $j$ 之间建一条无向边
2.对于每一个 $1≤i≤n$,找到一个最小的 $j$ 满足 $i<j≤n,a_j>a_i$,将 $i$ 和 $j$ 之间建一条无向边
注意:建立的边是在对应的下标 $i$,$j$ 之间建的边
请问有多少种长度为 $n$ 的排列 $a$ 满足,建出来的图含环
排列的数量可能会非常大,请输出它模上 $10^9+7$ 后的值
$n\leqslant 10 ^ 6$
思路
题面比较谜语人,大概翻译过来的意思就是,要找到含环的图的情况。但这样还是有点抽象,于是就反过来想。
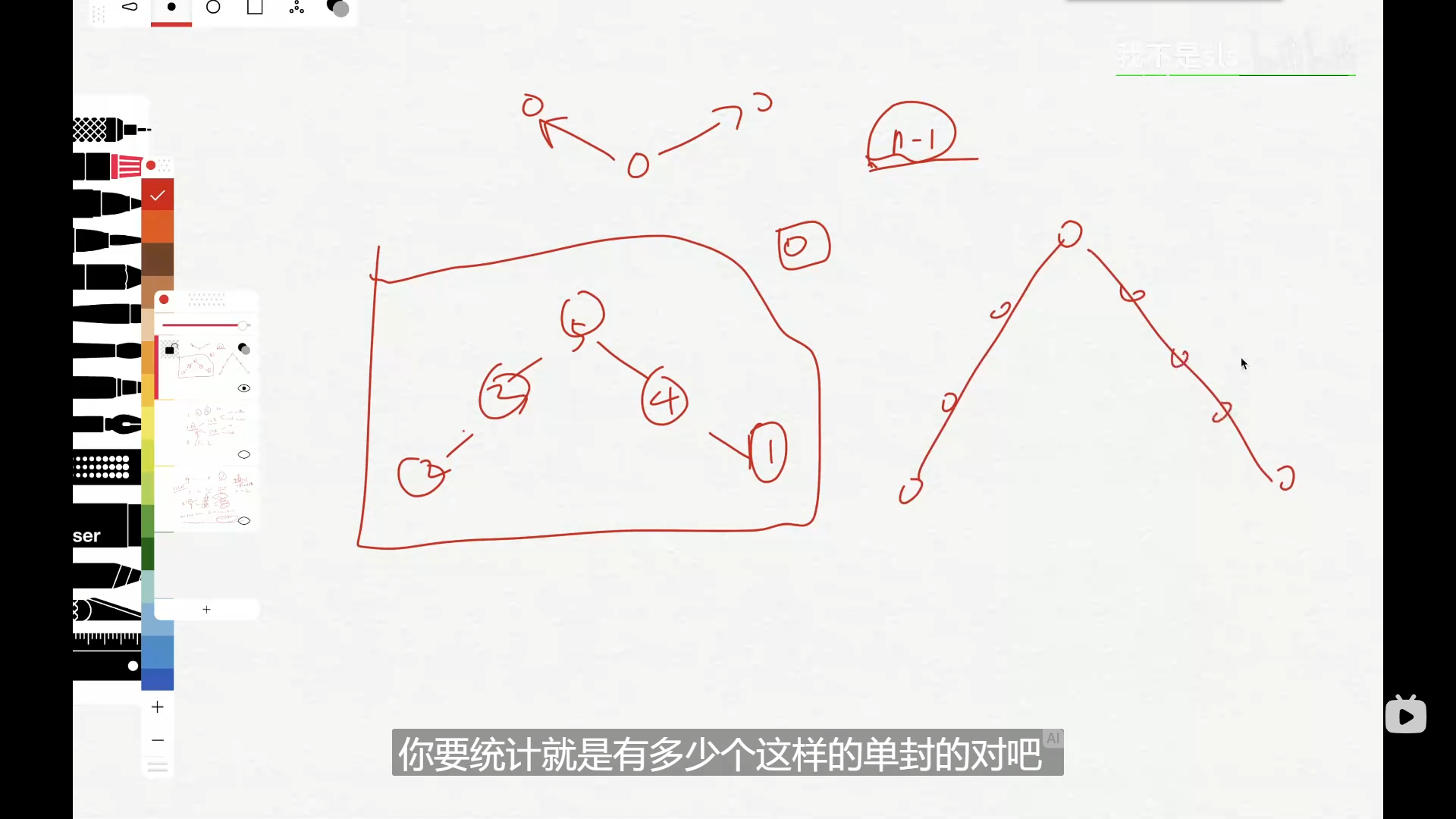
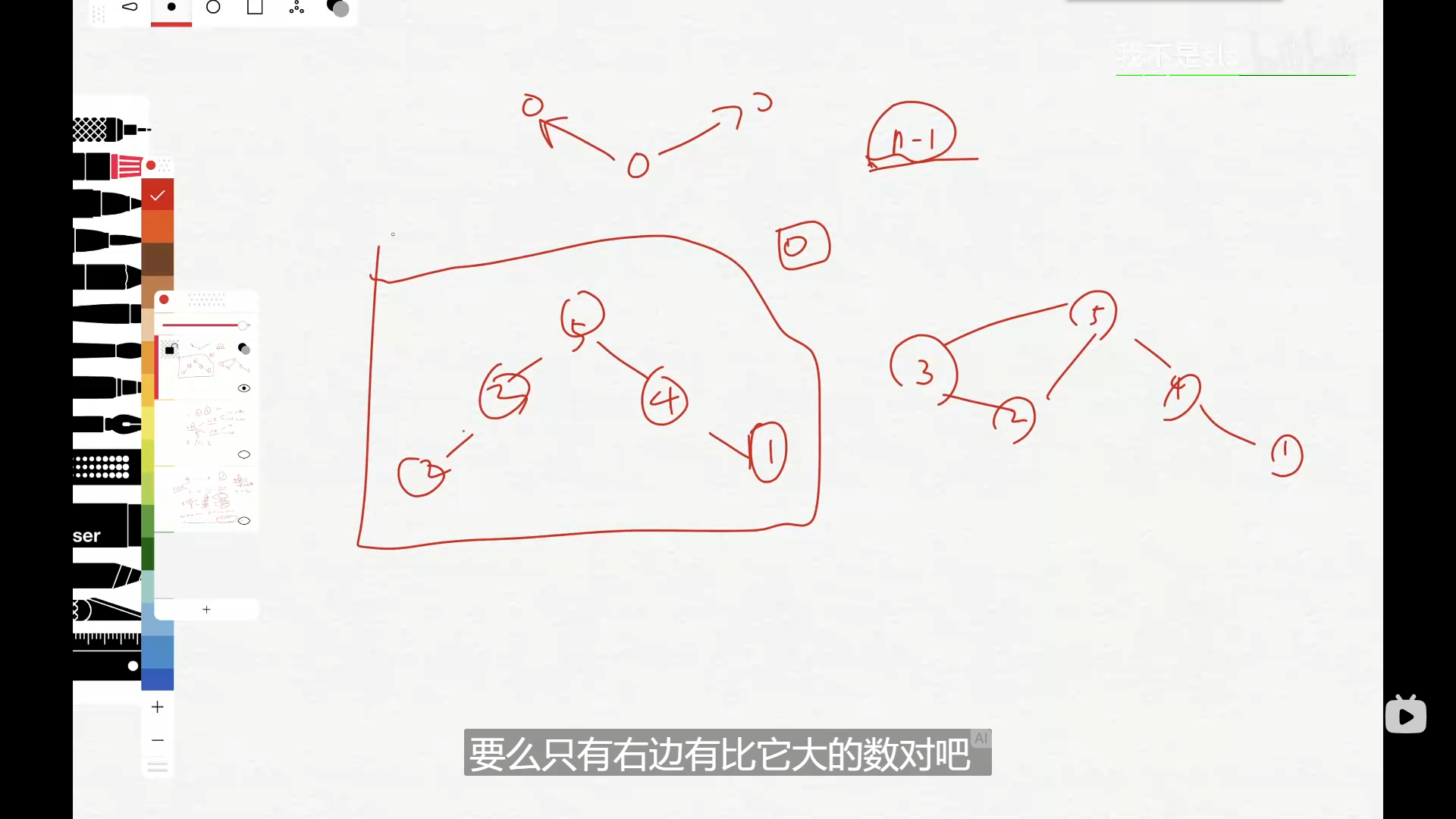
去寻找不含环的边,那么在题意中,不含环的图是这样的:
对于一个数,要么只在左边有比他大的,要么只在右边有比他大的
而只有一类图满足这种情况
说人话就是找以最大值为顶点的单峰的图有多少个
把这种情况去掉的情况就是含环的情况了
对$n$的全排列为$n!$,以最大值为顶点的单峰图有$2^{n - 1}$种情况(摆法):对于除了最大值的$n-1$个数,按降序摆放。每次摆放的时候都有在最大值左边和最大值右边两种选择,因此为$2^{n - 1}$
答案即为 $$n! - 2^{n - 1}$$
更多细节见代码(主要是取模)
代码
const int mod = 1e9 + 7;
const int N = 1e6 + 1;
ll f[N];
ll qmi(ll m, ll k, ll p){//求 m^k mod p,时间复杂度 O(logk)
ll res = 1 % p, t = m;
while (k){
if (k&1) res = res * t % p;
t = t * t % p;
k >>= 1;
}
return res;
}
void init(){//初始化处理阶乘数组
f[1] = f[0] = 1ll;
for (ll i = 2; i <= N; i++) {
f[i] = i * f[i - 1] % mod;
}
}
void solve(){
ll n;
cin >> n;
ll ans = qmi(2ll, n - 1, mod);
cout << (f[n] + mod - ans) % mod << endl; // 这个地方的 + mod 非常关键,防止负数,很多要取模的题都应注意
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int kase;
cin >> kase;
init();
while (kase--) {
solve();
}
return 0;
}
其实不太用得到快速幂,主要是在每次阶乘或平方的时候都要取模
不过刚好换个更好的快速幂板子了吧(
5.5
(待补)
题目链接
描述
给定$n$个点和$n-1$条路,镇从 $1$ 到 $n$ 依次编号,每条双向道路连接两个不同的村镇。接下来请你回答 $q$ 个问题,每次给出两个整数 $c, d$,表示现在分别有一个人在村镇 $c$,一个人在村镇 $d$,现在在 $c$ 的人要用最短的时间到达村镇$d$,在村镇 d 的人要以最短的时间到达村镇 $c$,假设两人同时出发,两人的速度也是一样的,每条双向道路的长度也是一样的,请问两人相遇的时候是在某一个村镇,还是在某条双向道路上?
$2≤n≤100000$
$1≤q≤100000$
对于每一个询问 $1 ≤ c_i < d_i ≤ n$
思路
这题拿到手最开始想的是就是一个简单的无向图求最短路然后判断奇偶,写了个BFS过了样例,自信满满交了一发,结果在第一个点就T飞了。
重新读了一遍题才发现询问次数$q$是$1e5$的,这样的话无论是BFS还是Dijkstra跑一趟都会超时,因为在每次询问的时候都要memset距离数组和used数组一次(后发现是自己BFS套板子套的太笨了,一样有人用BFS过了)
后在dls的建议下用LCA,因为$n-1$条路的话是树。套了个二月底写div1每日一题的LCA板子过了,但是还是晕晕乎乎的,有时间一定补!(顺便把代码用vector重构一下)
看了别人的代码才发现发现BFS是完全能做的,因为完全没有必要去求两点间的最短路,可以直接预处理根节点到每个节点的距离,再求距离差的奇偶性即可,这样也只需要一次memset了。
代码
const int N = 200005;
struct node{
int t, next;
}edge[2*N];
int a[N], head[N], tot, sum[N], depth[N], father[N][20];
void add(int x, int y){
edge[++tot].t = y;
edge[tot].next = head[x];
head[x] = tot;
}
void dfs(int u, int p){
sum[u] = sum[p] + a[u];
depth[u] = depth[p] + 1;
father[u][0] = p;
for (int j = 1; j < 19; j++) {
father[u][j] = father[father[u][j - 1]][j - 1];
}
for (int i = head[u]; i ; i = edge[i].next) {
int v = edge[i].t;
if (v == p)
continue;
else if (v != p){
father[v][0] = u;
dfs(v, u);
}
}
}
int LCA(int x, int y){
if (depth[x] < depth[y])
swap(x,y);
for (int i = 18; i >= 0; i--) {
if (depth[father[x][i]] >= depth[y])
x = father[x][i];
}
if (x == y)
return x;
for (int i = 18; i >= 0; i--) {
if (father[x][i] != father[y][i]) {
x = father[x][i];
y = father[y][i];
}
}
return father[x][0];
}
void solve(){
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) {
a[i] = 1;
}
for (int i = 1, u, v; i < n; i++) {
cin >> u >> v;
add(u,v);
add(v,u);
}
dfs(1,0);
for (int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v;
cout << ( (sum[u] + sum[v] - 2 * a[LCA(u, v)] )% 2 ? "Road" : "Town") << endl;
}
}
/* --------------------------------- BFS过法 ---------------------------------*/
const int N = 1e5 + 5;
vector<int>e[N];
int dis[N];
void bfs(){
memset(dis, -1, sizeof(dis));
dis[1] = 0;
queue<int>q;
q.push(1);
while (!q.empty()){
int t = q.front();
q.pop();
for(auto i : e[t]){
if(dis[i] == -1){
dis[i] = dis[t] + 1;
q.push(i);
}
}
}
}
void solve(){
int n, m;
cin >> n >> m;
for (int i = 0; i < n - 1; i++){
int x, y;
cin >> x >> y;
e[x].push_back(y);
e[y].push_back(x);
}
bfs();
int a, b;
while (m--) {
cin >> a >> b;
cout << ((abs(dis[a] - dis[b]) & 1) ? "Road" : "Town") << endl;
}
}
5.6
(代码待补)
题目链接
描述
现在给出一个表达式,形如 $a_1/a_2/a_3/…/a_n$。
如果直接计算,就是一个个除过去,比如 $1/2/1/4=1/8$。
然而小 A 看到一个分数感觉很不舒服,希望通过添加一些括号使其变成一个整数。一种可行的办法是 $(1/2)/(1/4)=2$。
现在给出这个表达式,求问是否可以通过添加一些括号改变运算顺序使其成为一个整数
$2≤n≤10000,1≤t≤100,1≤ai≤2^{31}−1$
思路
因为$a_2$前面的除号不能变成乘号,所以贪心的想,把后面除的数越变越小,再让$a_2$去除,才能得到最优解,因此用括号将$a_2$后面的括起来,即
$$a_1 / (a_2 / (a_3 / a_4…./a_n)) = a_1 \times a_3 \times…\times a_n / a_2 $$
这样的话就找每个数和$a_2$的gcd,只要有一个不是1就行
代码(copy)
void solve(){
int n;
cin >> n;
if (n == 1) {
puts("Yes");
return;
}
vector<int>a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
int temp = gcd(a[0], a[1]);
a[1] /= temp;
temp = a[1];
for (int i = 2; i < n; i++) {
if (temp > 1)
temp /= gcd(temp, a[i]);
}
cout << (temp == 1 ? "Yes" : "No") << endl;
}
5.7
(待补)
题目链接
描述
有一棵 $n$ 个节点的以1为根的有根树。现在可以对这棵树进行若干次操作,每一次操作可以选择树上的一个点然后删掉这个点和它的儿子之间的所有边。
现在想要知道对于每一个 $k∈[1,n]$,最少需要多少次操作才能让图中恰好存在 $k$ 个联通块。
输入格式
第一行输入一个正整数 $n$。
第二行输入 $n−1$ 个整数 $f_i$ 表示 $i+1$ 号点的父亲,保证 $1≤fi≤i$。
输出格式
输出 $n$ 个整数,第 $i$ 个数表示 $k=i$ 时的答案,如果无法让图中恰好存在 $k$ 个联通块,则输出$-1$。
思路
每减去一个节点,产生的联通块的数量就是该节点的孩子数量。 所以, 实质上是一道单重背包问题的变形。
代码(copy)
const int MAXN = 3005;
int n, max_x, root[MAXN], dp[MAXN];
void DP(){
for (int i = max_x; i >= 1; --i) {
if (root[i] != 0) {
for (int j = n; j >= root[i]; --j) {
if (dp[j - root[i]] != 0) {
if (dp[j] != 0) {
dp[j] = min(dp[j], dp[j - root[i]] + 1);
} else {
dp[j] = dp[j - root[i]] + 1;
}
}
}
}
}
}
void solve() {
int x;
cin >> n;
max_x = 0;
for (int i = 1; i < n; ++i) {
cin >> x;
root[x]++;
if (max_x < x) {
max_x = x;
}
}
dp[0] = 1;
DP();
for (int i = 0; i < n; ++i) {
if (dp[i]) {
cout << dp[i] - 1 << " ";
} else {
cout << -1 << " ";
}
}
printf("\n");
}
5.8
题目链接
描述
有一个长度为$n$的序列,现在我们想把它切割成三段(每一段都是连续的),使得每一段的元素总和都相同,请问有多少种不同的切割方法
思路
前缀和处理数组,从前往后扫一遍。切割成相同且连续的三段的话必然每个方案的切点都有$\dfrac{sum}{3}$和$\dfrac{2\times sum}{3}$且前者一定在右者的左边,这样一来,只需要记录三分之一处的数量,然后在每次遇见三分之二处的时候加上到目前为止的左端点的数量即可。
注意在$n$处不能当右端点。
代码
ll l, r, x, cnt = 0;
void solve(){
int n;
cin >> n;
vector<ll>a(n + 1);
for (int i = 1; i <= n; i++) {
cin >> x;
a[i] = a[i - 1] + x;
}
if (a[n] % 3){
cout << 0 << endl;
return;
}
l = a[n] / 3;
r = 2 * l;
x = 0;
for (int i = 1; i <= n; i++) {
if (a[i] == r && i < n)
cnt += x;
if (a[i] == l)
x++;
}
cout << cnt << endl;
}
5.9
题目链接
描述
给定整数 $n$,想将$1∼n$这$n$个数字分成两组,每一组至少有一个数,并且使得两组数字的和的最大公约数最大,请输出最大的最大公约数。
$n≤10^9$
思路
将$n$个数的和设为$sum$,每次分组,就是分为$x$和$sum-x$,题意即求$gcd(x,sum - x)$的最大值。
再次转化问题,即求$sum$最少能分成多少份,求此时让份数最小的$x$
代码
void solve(){
ll n;
cin >> n;
ll sum;
sum = (n + 1) * n / 2;
for (ll i = 2; i * i <= sum; i++) {
if (sum % i == 0) {
cout << sum / i << endl;
break;
}
}
}
5.10
题目链接
描述
给定一个长度为 $n$ 数组 $A$,执行以下操作 $m$ 次:
选择一段区间 $[l,r]$,将区间中所有的数加上整数 $x$。
操作完成后回答 $k$ 个问题:
每个问题给定一段区间 $[l,r]$,输出区间中所有数的和。
$1≤n≤2×10^5,1≤m,k≤10^5,|x|≤10^5$
思路
一眼差分加前缀和,不过这里注意要多用一个差分数组来记录,而不能直接在原数组上打标记,因为之后要进行前缀和操作。
时间复杂度为$O(n)$
代码
void solve(){
int n, m, k;
cin >> n >> m >> k;
vector<ll>a(n + 1);
vector<int>d(n + 1);
vector<ll>s(n + 1);
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
for (int i = 1; i <= n; i++) {
d[i] = a[i] - a[i - 1];
}
while (m--){
int l, r, x;
cin >> l >> r >> x;
d[l] += x;
d[r + 1] -= x;
}
for (int i = 1; i <= n; i++) {
a[i] = a[i - 1] + d[i];
s[i] = a[i];
s[i] += s[i - 1];
}
while (k--){
int l, r;
cin >> l >> r;
cout << s[r] - s[l - 1] << endl;
}
}
经典忘开LL然后WA了一发
看到个神仙做法,贴一下
signed main()
{
read(n);read(m);read(k);
for(int i=1;i<=n;++i) read(a[i]);
adjacent_difference(a+1, a+n+1, a+1);
while(m){
read(l); read(r); read(x);
a[l] += x;
a[r+1] -= x;
--m;
}
partial_sum(a+1, a+n+1, a+1);
partial_sum(a+1, a+n+1, a+1);
while(k){
read(l); read(r);
printf("%lld\n",a[r]-a[l-1]);
--k;
}
return 0;
}
看懂了adjacent_difference和partial_sum后写了个带注释版的
void solve2(){
int n, m, k;
cin >> n >> m >> k;
vector<ll>a(n + 1);
for (int i = 1; i <= n; i++) {
cin >> a[i];
}
adjacent_difference(a.begin() + 1, a.end(), a.begin() + 1);//将原数组变为差分数组
int l, r, x;
while (m--){
cin >> l >> r >> x;
a[l] += x;
a[r + 1] -= x;//在差分数组里面进行区间修改
}
partial_sum(a.begin() + 1, a.end(), a.begin() + 1);//将差分数组还原为原数组(后一项加前一项)
partial_sum(a.begin() + 1, a.end(), a.begin() + 1);//将原数组变化为前缀和
while (k--){
cin >> l >> r;
cout << a[r] - a[l - 1] << endl;
}
}
5.11
题目链接
描述
有一个 $01$ 序列,每次可以对其中的某一位取反($0$变$1$,$1$变$0$)
求最少翻转其中的几位可以使得该序列变为非递减序列
思路
不能相信这个题我昨天居然没看出来。。。最开始想的是找第一个$1$后面的$0$,每两个一组,数数就完了。
然后寄得很彻底,然后开摆了 然后甚至也没复习模电去看剧了
正确思路是找到$0$和$1$的分界点,分界点前面有$0$必须全是$0$,后面有$1$必须全是$1$。所以要分别找前面的$1$的数量和后面的$0$的数量。
用$a_i$记录到$i$点的前缀和,此分界点需要修改的数量为
$$a[i] + n - i - (a[n] - a[i])$$
扫一遍找最小值即可,复杂度是$O(n)$的
代码
void solve() {
int n;
cin >> n;
string s;
cin >> s;
vector<int>a(n + 1);
for (int i = 1; i <= n; i++) {
a[i] = a[i - 1] + s[i - 1] - '0';
}
int ans = INF;
for (int i = 0; i <= n; i++) {
ans = min(ans, a[i] + n - i - a[n] + a[i]);
}
cout << ans << endl;
}
感觉就是个div2A的题,已经是个废人了…
5.12
(待补)
题目链接
描述
约翰是一个农场主,他的农场有$n$块田,编号从 $1$到 $n$,这 $n$块田通过 $m$条双向道路相连(数据保证这$n$块田都是联通的),我们假设第$i$块田会产生 $2^i$$kg$ 的收益,现在约翰想把农田的工作全部交给自己的两个孩子,划分方式必须满足以下规则:
1.每一块田都需要恰好被分给一个孩子.
2.分给两个孩子的农田必须是联通的.就是说对于任意一个孩子在划分给自己的任意一块田,都可以不经过另外一个孩子的田,到达自己的任意一块田.
3.划分给两个孩子的收益必须尽可能的相等,如果无法相等,年长的孩子会得到大的那一份.
对于第 $i$块田,如果你要把它分给年长的孩子,请输出$A$,否则输出$B$.
$2≤n≤3e5,1≤m≤3e5$
思路
并查集
代码(copy)
class DSU{
vector<int> fa, sz;
public:
explicit DSU(int n ) : fa(n), sz(n){
iota(all(fa),0);
fill(all(sz),1);
}
int find(int i){
return i == fa[i] ? i : (fa[i] = find(fa[i]));
}
void join(int i, int j){
int a = find(i), b = find(j);
if (a == b)
return;
if (a > b)
swap(a, b);
fa[b] = a, sz[a] += sz[b];
}
int size(int i){
return sz[i];
}
};
void solve(){
int n, m;
cin >> n >> m;
DSU dsu(n);
while (m--){
int x, y;
cin >> x >> y;
x--,y--;
if (x != n - 1 && y != n - 1){
dsu.join(x, y);
}
}
string ans (n, 'A');
for (int i = 0; i < n - 1; i++) {
if (dsu.find(i) == dsu.find(n - 2))
ans[i] = 'B';
}
cout << ans << endl;
}
5.13
(待补)
题目链接
原题链接
描述
B 地区在地震过后,所有村庄都造成了一定的损毁,而这场地震却没对公路造成什么影响。但是在村庄重建好之前,所有与未重建完成的村庄的公路均无法通车。换句话说,只有连接着两个重建完成的村庄的公路才能通车,只能到达重建完成的村庄。
给出 B 地区的村庄数 $N$,村庄编号从 $0$ 到 $N-1$,和所有 $M$ 条公路的长度,公路是双向的。并给出第 ii 个村庄重建完成的时间 $t_i$,你可以认为是同时开始重建并在第 $t_i$天重建完成,并且在当天即可通车。若 $t_i$为 $0$ 则说明地震未对此地区造成损坏,一开始就可以通车。之后有 $Q$ 个询问 $(x,y,t)$,对于每个询问你要回答在第 $t$ 天,从村庄 $x$ 到村庄 $y$ 的最短路径长度为多少。如果无法找到从 $X$ 村庄到 $y$ 村庄的路径,经过若干个已重建完成的村庄,或者村庄 $x$ 或村庄 $y$ 在第 $t$ 天仍未重建完成,则需要返回 -1
思路
Floyd
代码(Copy)
#define N 205
int n,m;
int a[N];
int f[N][N];//邻接矩阵存边
inline void updata(int k){
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
if(f[i][j]>f[i][k]+f[j][k])
f[i][j]=f[j][i]=f[i][k]+f[j][k];//用这个新的更新所有前面的
return;
}
int main(){
cin>>n>>m;
for(int i=0;i<n;i++)
scanf("%d",a+i);//依次输入每一个村庄建立完成时需要的时间
for(int i=0;i<n;i++)
for(int j=0;j<n;j++){
f[i][j]=1e9;//初始化为保证它不爆炸范围内的最大值
}
for(int i=0;i<n;i++)
f[i][i]=0;
int s1,s2,s3;
for(int i=1;i<=m;i++){
scanf("%d%d%d",&s1,&s2,&s3);
f[s1][s2]=f[s2][s1]=s3;//初始化边长
}
int q;
cin>>q;
int now=0;
for(int i=1;i<=q;i++){//处理各询问
scanf("%d%d%d",&s1,&s2,&s3);
while(a[now]<=s3&&now<n){
updata(now);//依次更新点,使它可以被用来更新其他的点
now++;
}
if(a[s1]>s3||a[s2]>s3)cout<<-1<<endl;
else {
if(f[s1][s2]==1e9)cout<<-1<<endl;
else cout<<f[s1][s2]<<endl;
}
}
return 0;
}