此纪录从2022-10-21 09:56:46始
Educational Codeforces Round 142
C. Min Max Sort
题意
给定一个排列,选择两个值,将其中较小的值移到排列首部,较大的值移到排列尾部。求将排列排序为严格递增序的最小操作次数。
思路
这题本来是在vp的时候用双指针分情况讨论做的,然后发现戴老师的dp做法很炫酷,所以还是补一下
双指针做法
首先最终的有序序列中,$(1, n), (2, n - 1)$这种成对的数字一定是关于数组的中心点对称的,因此在操作的时候也要选这对数字来分别插入到两边才能实现目标。
对于任意一个排列,最多操作$\lfloor \frac{n}{2} \rfloor$次。做法就是先记录排列中每个数字在原数组中的位置,然后从中间数据的位置开始往两边扫,如果符合要求,则说明这对数字不用动,$ans -= 1$
DP做法(待补) 最长上升子序列
代码
"""
双指针做法
"""
def solve():
n = int(input())
a = list(map(int, input().split()))
p = [0] * (n + 1)
for i in range(n):
p[a[i]] = i + 1
if a == sorted(a):
print(0)
return
ans = 0
if n & 1 == 0:
# print(p)
ans = n // 2
l = n + 1
r = 0
for i in range(n // 2):
ll = n // 2 - i
rr = n // 2 + i + 1
if p[ll] < p[rr] and p[ll] < l and p[rr] > r:
l = p[ll]
r = p[rr]
ans -= 1
else:
break
else:
ans = n // 2
l = r = p[n // 2 + 1]
for i in range(1, n // 2 + 1):
ll = n // 2 + 1 - i
rr = n // 2 + 1 + i
if p[ll] < p[rr] and p[ll] < l and p[rr] > r:
l = p[ll]
r = p[rr]
ans -= 1
else:
break
print(ans)
D. Fixed Prefix Permutations
题意

思路
字典树,看的ygg题解qwq


在字典树的insert()操作时,将当前列表的pos数组给插入进去,这样,在查询操作时,就能查询整个字典树中能和自己匹配的最大前缀数量。
代码
idx = 0
def solve():
n, m = map(int, input().split())
trie = [[0] * 11 for _ in range(10 * n)]
global idx
idx = 0
def insert(s):
global idx
p = 0
for c in range(1, m + 1):
if trie[p][pos[c]] == 0:
idx += 1
trie[p][pos[c]] = idx
p = trie[p][pos[c]]
def query(s):
p = 0
cnt = 0
for c in s:
if trie[p][c] != 0:
p = trie[p][c]
cnt += 1
else:
break
return cnt
a = []
for i in range(n):
pos = [0] * 11
a.append(list(map(int, input().split())))
for j, x in enumerate(a[i]):
pos[x] = j + 1
insert(a[i])
for x in a:
print(query(x), end=" ")
print()
另外需要注意的一点就是Trie的数组大小,当前来看第一位开$10 * n$不会越界,但最开始在每个solve里面开$1e5$又会T(acwing的板题都没有多组数据= =
1.28注:Trie的数组第一维一般是开$n * d$(d是最大可能深度)
Educational Codeforces Round 141
这场是真的狠狠被教育了…B的构造手玩半天没玩出来,有思路之后写蛇形矩阵的实现写了一万年…真的叫基础不牢地动山摇
C. Yet Another Tournament
题意
有$n$名玩家,战力分别为$[1, n]$。我们也是一名玩家,一共有 $n+1$ 名玩家。对于 $n$ 名玩家来说, $i$ 能击杀 $j$ 当且仅当 $i > j$ 。对于每一位玩家我们都有一个准备值 $a_i$ ,我们想要击败该名玩家需要花费 $a_i$ 的时间去准备。刚开始我们拥有的时间为 $m$ ,每名玩家都和其余所有玩家进行一轮对局,最终按照胜场数量对所有玩家进行排名,求我们合理分配时间会获得的最高排名。
思路
经典读错题,看到题里面的 Calculate the minimum possible place (lower is better) ,以为名次要越低越好…
可以二分/贪心,感觉贪心好想一点,其实二者本质上是一样的。
策略是选择尽量多的选手,因此先将选手排序。
然后关键在于自己最后赢的一个人,要找和自己名次相同的那个人(别人的名次是可以计算的),因为如果能放弃自己为前一个人(自己准备时间的最尾端)准备的时间来准备跟与自己相同名次的人比赛,如果时间充足,即可胜利,排名上升一名。反之排名不变,也没损失。
因为在最后一次的决定中,放弃与前一个人的准备时间并不会让自己的排名下降。如果前一个人的排名比自己低,那结果是两人都上升一名,若等于或高于自己的排名,则不会发生变化。
如果时间不够就不用放弃
代码
def solve():
n, m = map(int, input().split())
a = list(map(int, input().split()))
b = a.copy()
b.sort()
win = 0
while win < n and b[win] <= m:
m -= b[win]
win += 1
if win == n:
print(1)
return
if win == 0:
print(n + 1)
return
if m + b[win - 1] - a[win] >= 0:
print(n - win)
else:
print(n - win + 1)
D. Different Arrays
题意
给定一个长度为n的数组,必须进行$n ― 2$次操作,对$[2, n 一1]$范围内的数按顺序进行一次操作,一次操作为让左边和右边的两个数一个加上$a_i$一个减去$a_i$; ($a_i$指的是当前值),求操作后可能获得的数组的数量。
$$0≤a_i≤300, 1≤n ≤300$$
思路
看典哥题解写的…一开始还以为py用二维会炸(事实上也在炸的边缘),后来发现是自己太相信py的高精度了,被狠狠教育了
如果把结果放在最后才%MOD,可能会TLE或MLE
dp,看值域考虑dp,所有数最终能够变成的值域是$[-300 * 300, 300 * 300]$
二维版本
$f[i][j]$ 表示前$i$个数中,最终凑成的值$j$的方案数
每次先循环位置,再枚举当前位置最终变成的数
转移方程:
$$f[i + 1][a[i + 1] + j] += f[i][j]$$
$$f[i + 1][a[i + 1] - j] += f[i][j]$$
坑点:如果j = 0的话就只需要转移一次,要特判一下
一维版本
其实思路一样,不过是类似滚动数组,每遍历到一个$a_i$的新位置,用一个新数组存,然后覆盖老数组,就可以去掉$i$的维度。这样写居然不会MLE我也觉得很神奇
代码
def solve():
N = 310
n = int(input())
a = list(map(int, input().split()))
# f[i][j] = 前i个数中,最终变成的数为j 的方案数
f = [[0] * 90250 * 2 for _ in range(N)]
p = 90000
# 初始化,最开始只有位置2,值域也只能到a[2]
f[1][a[1] + p] = 1
for i in range(1, n - 1):
# 对于每个a_i,试探所有可能值(若在a_i前面的值使f[i][j]不为空,说明前i个数能够到达j这个值)
for j in range(-p + 300, p - 300 + 1):
if f[i][j + p] != 0 and j != 0:
f[i + 1][a[i + 1] - j + p] += f[i][j + p]
f[i + 1][a[i + 1] - j + p] %= 998244353
f[i + 1][a[i + 1] + j + p] += f[i][j + p]
f[i + 1][a[i + 1] + j + p] %= 998244353
elif f[i][j + p] != 0:
f[i + 1][a[i + 1] + p] += f[i][j + p]
f[i + 1][a[i + 1] + p] %= 998244353
ans = 0
for i in range(-p, p):
ans += f[n - 1][i + p]
ans %= 998244353
print(ans)
# 一维版本
def solve2():
n = int(input())
a = list(map(int, input().split()))
MOD = 998244353
p = 90005
ans = [0] * (2 * p + 500)
ans[a[1] + p] = 1
for i in range(n - 2):
dp = [0] * (2 * p + 500)
for j in range(-p, p + 1):
if ans[j + p] and j != 0:
dp[a[i + 2] + j + p] += ans[j + p]
dp[a[i + 2] + j + p] %= MOD
dp[a[i + 2] - j + p] += ans[j + p]
dp[a[i + 2] - j + p] %= MOD
elif ans[j + p]:
dp[a[i + 2] + p] += ans[j + p]
dp[a[i + 2] + p] %= MOD
ans = dp
print(sum(ans) % MOD)
这题的教训就是一定记得计算需要的数组长度(济南的签到好像也是这样栽了半天),和ans不要留到最后才模
Educational Codeforces Round 140
C. Count Binary Strings
题意
给定一个01串,给定每一个区间范围内的限制。其中 g[i][j]表示对于区间[i, j]的限制。若g[i][j] = 1,说明这个区间内只能出现一种数;若g[i][j] = 2,说明这个区间内必须同时出现两种数;若g[i][j] =0,说明这个区间没有限制。求合法01串的数量。
思路
DP,观察发现若为合法01串,对于指定的右端点r,一定有:$a[1][r], a[2][r]…a[r][r]$呈现$2222…111..1$的特征。因为从后往前考虑,如果r - 1的位置与r的位置相同,则$a[r - 1][r] = 1$,否则为2。而一旦有某个位置为2了,这个位置往前的所有位置都会是2。
令$dp[i][j]$表示在前i个位置中,分界点为$j$的方案数(即,$j$以前为$2$,$j$及以后为$1$),答案为在位置$n$时的所有分界线位置方案之和,即 $$\sum_{i = 1}^{n}dp[n][i]$$
转移:从$dp[i][j]$开始,如果向后摆放的是和上一位相同的数,则j不变,转移到$dp[i + 1][j]$。若向后摆放的是和上一位不同的数,则$j$直接跳到$i + 1$,转移到了$dp[i + 1][i + 1]$。转移方程:
$dp[i + 1][j] += dp[i][j]$
$dp[i + 1][i + 1] += dp[i][j]$
注意这题还需要一个判断合法条件的操作,因为如果在$[1,j - 1]$区间有不该出现的$1$或在$[j, n]$区间有不该出现的$2$,则说明$j$在这个位置分割的方案是不可达到的,需要将该位置的$dp[i][j]$置$0$。
代码
def solve():
n = int(input())
a = [[0]]
dp = [[0] * (n + 2) for _ in range(n + 2)]
MOD = 998244353
for i in range(1, n + 1):
a.append([0] * i + list(map(int, input().split())))
dp[1][1] = 2 # 表示第一个位置可以为1可以为0
# l是分界点的坐标,在遍历前r个时,枚举分界点坐标
for r in range(1, n + 1):
for l in range(1, r + 1):
flag = 0
for k in range(1, l):
if a[k][r] == 1:
flag = 1
for k in range(l, r + 1):
# print(k, r)
if a[k][r] == 2:
flag = 1
if flag: dp[r][l] = 0 # 说明此处不合法,不满足22221111...
# print(r + 1, l)
dp[r + 1][l] = (dp[r + 1][l] + dp[r][l]) % MOD
dp[r + 1][r + 1] = (dp[r + 1][r + 1] + dp[r][l]) % MOD
ans = 0
for i in range(1, n + 1):
ans = (ans + dp[n][i]) % MOD
print(ans)
Educational Codeforces Round 139
D. Lucky Chains
题意
给定两个数$a, b(1 \leq a, b \leq 1e7)$,执行如下语句:
while(gcd(a, b) == 1) a++, b++, cnt++ ;
求cnt的值
思路
数学苦手,看典哥题解都理解了好一会
一个gcd的性质
$gcd(a, b) == gcd(a, b - a)$
假设 $a$ 是更小的那个数,我们根据gcd的性质推导一下: $gcd(a, b) == gcd(a, b - a)$ 因此 $gcd(a + k, b + k) == gcd(a + k, b - a)$ 。
$b - a$是一个定值,因此问题转化成对于每一个$ b - a $的质因数$p$(刚开始还想了半天为什么找质因数,菜死了),$(a + k) % p == 0$ 时$k$的最小值,式子可转化为求$a - a%p$ 的最值。
一种更快的办法是直接找每个数的最小质因子,然后对$p$进行除的操作来找到其下一个质因数,这样就不用处理所有的质数
前者复杂度为$O(nsqrt(n))$,因为需筛出所有的质数
后者为$O(nlog(n))$
代码
primes = [-1] * 10 ** 7
def init():
# 所有数的最小质因子
for i in range(2, 10 ** 7):
if primes[i] == -1:
for j in range(i, 10 ** 7, i):
primes[j] = i
def solve():
a, b = map(int, input().split())
dif = b - a
if dif == 1:
print(-1)
return
if math.gcd(a, b) != 1:
print(0)
return
if dif & 1 == 0:
print(1)
return
ans = dif - a % dif
while dif != 1:
ans = min(ans, primes[dif] - a % primes[dif])
# 找到下一个质因数
dif //= primes[dif]
# print(primes[1:25])
print(ans)
if __name__ == "__main__":
init()
for test_case in range(1, int(input()) + 1):
solve()
贴一个前一天的C,是相似的题,一起补了
题意
给定一个数列$a$,问是否存在$i, j$使得$gcd(a_i, a_j) \neq 1$
思路
思路差不多,主要也是考察的筛
不过数据范围是$1e9$,直接根号筛的话用py过不去,因为C++都跑了1100ms
看了下别人的py代码没太看懂,也许需要更高级的筛法,比如用随机化筛,能变成$O(M^{\dfrac{1}{4}})$, 但没存py的板子也没必要存,就直接换C++用$O(\sqrt{M})$的筛法莽过去了
const int N =33333;
vector<int>primes(N, 0);
vector<int>vis(N, 0);
void init() {
int now = 0;
for (int i = 2; i < N; i++) {
if (!vis[i]) primes[now++] = i;
for (int j = 0; primes[j] * i < N; j++) {
vis[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
void solve(){
int n;
cin >> n;
vector<int>a(n);
for (int i = 0; i < n; i++) {
cin >> a[i];
}
for(auto i : primes){
if (i == 0){
break;
}
int cnt = 0;
for (int j = 0; j < n; j++) {
if (a[j] % i == 0){
cnt++;
while (a[j] % i == 0){
a[j] /= i;
}
}
}
if (cnt >= 2){
cout << "YES" << endl;
return;
}
}
map<int, int>mp;
for (int i = 0; i < n; i++) {
if (a[i] != 1){
mp[a[i]]++;
}
if (mp[a[i]] >= 2){
cout << "YES" << endl;
return;
}
}
cout << "NO" << endl;
}
Educational Codeforces Round 138
C Number Game
题意:
给定一个长度为$n$的整数数组$a$, Alice和Bob玩游戏.对于一个$k$, 游戏进行$k$轮, 第$i$轮,Alice选择从a中删除一个小于等于$k - i + 1$的数, Bob选择一个数加上$k - i + 1$.如果某一轮Alice没有数字可以选择,则Bob赢,否则Alice赢.问使得Alice赢的最大的k是多少?
$(n <= 100)$
思路
最开始以为是二分答案,但注意到n比较小,所以可以直接写模拟,Bob的策略应该是每回合将Alice当前的$k - i + 1$加到当前数列的最小项上面,这样能最大化减少Alice能删掉的数量。Alice的策略则是趁$k - i + 1$减小之前每次尽可能删掉能删掉的最大数。
其实这个思路很好想,昨晚在看题十分钟后就想到了,但写模拟代码写了一万年还调错了,典中典之脑子会了手没会。
今早想清楚模拟过程之后10分钟1A了
代码
$O(n^3)$
def solve():
n = int(input())
b = list(map(int, input().split()))
b.sort()
k = n
while k > 0:
a = b.copy() # 最开始写的 a = b,没发现,调其他地方调了一万年
index = 1
while index <= k:
pos = -1
temp = k - index + 1
for i in range(len(a)):
if temp >= a[i]:
pos = i
if pos == -1:
k -= 1
break
if index == k:
print(k)
return
a.remove(a[pos])
if len(a) > 0:
a[0] += temp
a.sort()
index += 1
print(k)
$O(nlogn)$ 待补
void solve() {
int n;
cin >> n;
vector<int> a(n);
cin >> a;
sort(a.begin(), a.end());
int left = 0, right = (n + 1) / 2;
auto check = [&](int k) {
if (k == 0) return true;
if (a[k - 1] != 1) return false;
for (int i = k; i < 2 * k - 1; i++) {
if (a[i] > i - k + 2) {
return false;
}
}
return true;
};
while (left <= right) {
int k = (left + right) / 2;
if (check(k)) left = k + 1;
else right = k - 1;
}
cout << left - 1 << "\n";
}
D. Counting Arrays
在problemset里面看到一道1k9的dp,想做做…结果发现是数学…线筛的一个地方抄错了找了2h…相似
题意
给定一个 n 和 m ,构造出一个长度为n,每一个元素的范围是[1, m]的数组,求有多少个数组是模棱两可的。一个模棱两可的数组的定义是其删除数组b不唯一,($b_i$是第i次操作时的删除数)一个元素a[i]可以被删除当且仅当$gcd(a[i], i) == 1$。
思路
正难则反,一共只有模棱两可和删除数组唯一两种情况。而删除数组唯一时,b数列一定全为1。说明在删除数组唯一的情况下,$a_i$去模范围$[2, n]$内的所有质数一定不为1。(都不互质)
进而推得$a_i$ 的值域一定是$[2, n]$内的所有质数的质数积及其倍数
设枚举到$i$时的质数积为$temp$,则个数为$\left \lfloor \frac{m}{temp} \right \rfloor$
然后利用乘法原理统计即可。最后的答案是总方案数减去删除数组唯一的数量。
注意题目求的是长度为$[1, n]$区间所有长度的a的模棱两可数量,因此在每算一次就要加到ans上,而不是最后用n长度时的sum-cnt(sb题面)
代码
maxn = 3 * 10 ** 5 + 5
isPrime = [0] * maxn
primes = [0] * maxn
def init():
cnt = 0
isPrime[1] = 1
for i in range(2, maxn):
if isPrime[i] == 0:
primes[cnt] = i
cnt += 1
j = 0
while i * primes[j] < maxn:
isPrime[i * primes[j]] = 1
if i % primes[j] == 0:
break
j += 1
def solve():
n, m = map(int, input().split())
MOD = 998244353
ans = 0
temp = 1
mul = 1
for i in range(1, n + 1):
if isPrime[i] == 0:
temp *= i
if temp > m:
break
mul *= (m // temp) % MOD
ans += mul % MOD
__sum = 0
for i in range(1, n + 1):
__sum += pow(m, i, MOD)
__sum %= MOD
print((__sum - ans) % MOD)
Educational Codeforces Round 134
D. Maximum AND
题意
给定两个数列$a$, $b$, 令$c_i = a_i \bigoplus b_i$, 定义价值为 $c_1$ & $c_2$ & $c_3$& … $c_n$ 求价值的最大值
$(1≤n≤10^5)$ $(0≤a_i, b_i<2^{30})$
思路
注意到c在某一位为1时只能是当所有的$c_i$在这一位都为1才能取到,进而需要所有匹配的$a_i$ 和 $b_i$在这一位的异或都为1。
那么如何找这样满足条件的匹配呢,看题解发现有一种很妙的方法可以实现。$c$贪心地从最高位为$1$开始往下取,然后先假设$c$这一位为1,通过map计数check是否所有的$a_i, b_i$都能满足条件,而并不需要排列来对每个$i$进行匹配。
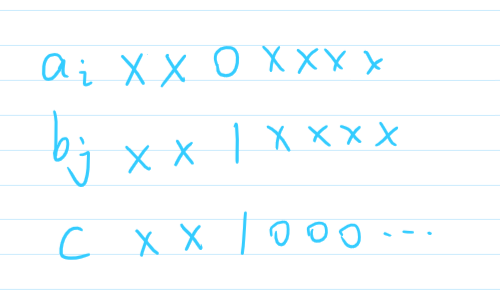
如上图所示,如果存在一组满足这样关系的a和b,则用map计数添加进去,而如果c在这一位能够取到1的话,那么map的value一定是一个确定值。
最后再让$c |= (1 « i)$(更新值),继续往后推:在这样的高位取值下,c的低位取值情况即可
def solve():
n = int(input())
a = list(map(int, input().split()))
b = list(map(int, input().split()))
d = defaultdict(int)
ans = 0
for i in range(30, -1, -1):
temp = ans | (1 << i)
d.clear()
ok = 1
for j in range(n):
d[a[j] & temp] += 1
d[~b[j] & temp] -= 1 # 判断是否异或为1
for j in d.values():
if j != 0:
ok = 0
break
if ok != 0: # 如果能取到才用或运算加上值
ans = temp
print(ans)
Educational Codeforces Round 131
D. Permutation Restoration
题意
Educational Codeforces Round 124
D. Nearest Excluded Points
题意
给定$n$个两两不同的整点坐标,对于每个整点$p$,求:不包含在这 $n$ 个点内的其他整点中,与点 $p$ 距离最近的那个。
思路
答案肯定不能搜寻整个平面,通过观察得,答案只可能在$n$个点组成的图形的“边缘”处
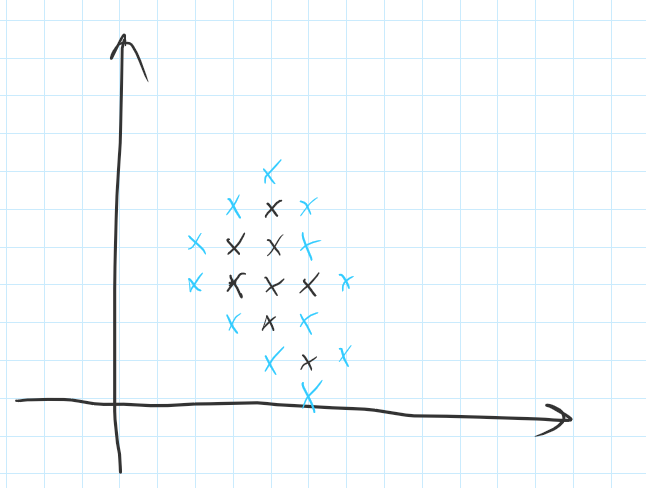
使用多源bfs来进行搜索,先将图形边缘的所有点加入队列中然后再依次进行广搜。注意,因为有较内层的点,因此就算搜到了在给定的$n$个点内的坐标也要加入队列,然后依次传递答案(更近的点一定更快传递到中心)
不是很懂为什么是1900的题,可能赛时大家都没想到从边缘开始搜(?
更多细节见代码
from collections import defaultdict, deque
def solve():
n = int(input())
dir = [(1, 0), (-1, 0), (0, 1), (0, -1)]
points = []
res = dict()
for i in range(n):
x, y = map(int, input().split())
points.append((x, y))
res[points[-1]] = None
q = deque()
for x, y in points:
for dx, dy in dir:
nx, ny = x + dx, y + dy
if (nx, ny) not in res:
q.append((nx, ny))
res[(nx, ny)] = (nx, ny)
while q:
x, y = u = q.popleft()
for dx, dy in dir:
v = x + dx, y + dy
if v in res and res[v] is None:
# print(v, u, res[v], res[u])
q.append(v)
res[v] = res[u]
for x in points:
print(*res[x])
Educational Codeforces Round 112
D. Say No to Palindromes(DP)
题意
给定一个由a,b,c组成字符串,定义一个字符串是美丽的当且仅当它的字串中没有回文。
$m$次询问,每次给定左右端点$l, r$,如果此字符串不美丽,则每修改一个字符cost+=1,问使将这一段字符串修改成美丽字符串的最小花费是多少。
$(1≤n,m≤2⋅10^5)$
思路
注意到对于每个$s_i$, $s_i \neq s_{i - 1}$并且$s_i \neq s_{i - 2}$才能不形成回文,由于一共只有三种字母,所以$s_i$一定等于$s_{i - 3}$,因此,修改后的整个字符串一定是"abcabcabc…" 或"bacbacba…" 等共六种排列情况的串。
然后在询问前把6种字符串修改情况的操作次数前缀和一下,s[i]代表字符串修改到$i$时的修改次数,在每次询问时用s[r] - s[l - 1]就是这种排列情况时的需要修改的次数(不用关心具体修改了哪些),然后取6个情况中的最小值即可,查询复杂度为$O(1)$
因为一共就三种字符,所以6种情况一定可以覆盖完全
代码
def solve():
n, m = map(int, input().split())
s = input()
lis = ['abc', 'acb', 'bca', 'bac', 'cab', 'cba']
dp = [[0] * (n + 1) for i in range(6)]
for i in range(6):
for j in range(n):
dp[i][j + 1] = dp[i][j]
if s[j] != lis[i][j % 3]:
dp[i][j + 1] += 1
for _ in range(m):
x, y = map(int, input().split())
ans = 114514114514
for i in range(6):
ans = min(ans, dp[i][y] - dp[i][x - 1])
print(ans)
Educational Codeforces Round 110
C. Unstable String
题意
给一个字符串,其含有$0,1,?$. 其中,$?$可以看成$1$,也可以看成$0$。如果一个字符串可以是0和1交替出现的,就称这个字符串是$beautiful$。问现在这个字符串有多少$beautiful$的子串?
例如,
字符串$1,10$是beautiful的;
字符串$1???1$也是beautiful的,因为通过问号可以转化为10101;
但字符串$1???1$不是beautiful的,因为通过问号不管怎么变,都不可能使得01交替出现。
思路
最开始拿到手感觉很容易想到用奇偶去做,但是想不出来,找题解用dp做了
由于需要统计子串的数量,考虑统计每一位的贡献去做。
今天稍微又理解了一下贡献的概念,比如长度为$1$有$1$个子串,增加到$2$时新增了$dp[i] + 1 = 2$条子串,那长度为$2$的字符串一共就有$dp[1] + dp[2] = 3$ 条子串($dp[i]$代表新增到第$i$个时对答案的贡献)
用$dp[i][0]$和$dp[i][1]$分别表示以第$i$个数结尾,$s[i]$选$0$和选$1$的集合。属性是:新增摆放$s[i]$后,新增的合法子串数目(也即对答案的贡献)
转移分两种情况:
1、如果$a[i] = ?$,则$dp[i - 1]$的两种情况都能转移
$$dp[i][1] = dp[i - 1][0] + 1$$
$$dp[i][0] = dp[i - 1][1] + 1$$
2、如果为0或者1,则只转移一种,以 $1$ 为例,上一项为 $1$ 这一项为 $0$ 的构造是不可能的,因此,令当前项为0的构造方案也就不存在了,要重新置零开始。
$$dp[i][1] = dp[i - 1][0] + 1$$
$$dp[i][0] = 0$$
注意每次转移时需要取一个$max(dp[i][1], dp[i][0])$加在$ans$上。
代码
def solve():
s = '.' + input()
n = len(s)
dp = [[0] * 2 for _ in range(n + 1)]
dp[1][0] = 1 if s[1] != '1' else 0
dp[1][1] = 1 if s[1] != '0' else 0
# print(s[1], dp[1][0])
ans = max(dp[1][0], dp[1][1])
for i in range(2, n):
if s[i] == '?':
dp[i][0] = dp[i - 1][1] + 1
dp[i][1] = dp[i - 1][0] + 1
elif s[i] == '0':
dp[i][0] = dp[i - 1][1] + 1
elif s[i] == '1':
dp[i][1] = dp[i - 1][0] + 1
ans += max(dp[i][1], dp[i][0])
# print(dp)
print(ans)
Educational Codeforces Round 106
C. Minimum Grid Path
待补
