ABC287
D - Match or Not
题意
给定两个由小写字母和?字符串$S,T$, 问$S’$和$T$是否匹配,其中,$S′$由 $S$串的前 $x$个字符和后 $|T|−x$个字符组成。
两个字符串匹配,当且仅当将其中的 ?替换成英文字母后,两个字符串相同或他们本身就相同。
思路
两个字符串匹配,当且仅当每一位要么是相同字母,要么至少有一个?。于是我们可以储存所有不满足这些条件的位置。当且仅当该位置的数量为0时,两个字符串匹配。
注意到当$x$递增的时候,前后两个 $S′$ 仅有一个位置不同,因此我们可以继承上一个状态,仅判断变化的位置能否匹配即可。
答案一定呈现NO YES … YES YES YES …NO NO NO 或 YES YES YES … NO NO NO 这样的分布,即第一次由YES变成NO之后不可能回到YES
代码
def solved():
s = input()
t = input()
n = len(s)
m = len(t)
se = set()
now = 0
for i in range(n - m, n):
if s[i] != "?" and t[now] != "?" and s[i] != t[now]:
se.add(now)
now += 1
print("Yes" if len(se) == 0 else "No")
for i in range(m):
try:
se.remove(i)
except:
pass
if s[i] != "?" and t[i] != "?" and s[i] != t[i]:
se.add(i)
print("Yes" if len(se) == 0 else "No")
E - Karuta
题意
给定$n$个字符串,对于每个字符串 $s_i$,问 $maxLCP(si,sj)_{i≠j}$,其中$LCP$是最长公共前缀。
思路
其实只需要排序一次,最长公共前缀一定能出现在字典序上的邻居两个字符串之间。
代码
def solvee():
n = int(input())
s = []
for i in range(n):
s.append([input(), i])
s.sort()
ans = [0] * n
def check(a, b):
now = 0
l = min(len(a), len(b))
while now < l and a[now] == b[now]:
now += 1
return now
for i in range(n):
if i == 0:
ans[s[i][1]] = check(s[i][0], s[i + 1][0])
continue
if i == n - 1:
ans[s[i][1]] = check(s[i][0], s[i - 1][0])
continue
ans[s[i][1]] = max(check(s[i][0], s[i - 1][0]), check(s[i][0], s[i + 1][0]))
print(*ans, sep="\n")
ABC295
D - Three Days Ago
题意
给定一个字符串$S$,找出区间$[L, R]$的个数,使$S_LS_{L + 1}…S_R$中每个数字出现的次数为偶数
思路
开始的思路想的是用前缀和记录下次数,然后乱搞搞,但是想想觉得会写的很答辩。就直接逃跑看题解了…
有篇题解写的特别简洁,偷了贴出来
我们只关注出现的奇偶性所以显然可以只维护这个前缀里每个字母出现奇数还是偶数次,也就是直接状压,设状态为 S,则只有前面的状态 S才可以与当前的状态 S相匹配形成一个符合条件的区间,所以直接扫一遍维护一下就好了。
说人话就是,可以用十位二进制数存到目前位置的数字出现情况,每次回到这样的出现次数状态就说明异或为0(或者1, 与初值有关)了,记录回到这样状态的次数(即某些数字出现了偶数次了且其他数字出现情况(前缀)都相同),累加一下,就能做到只扫一遍就把所有情况都统计完了。
例(v的变化情况):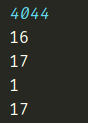
代码
def solved():
s = input()
v = 0
cnt = [0] * (1 << 11)
n = len(s)
ans = 0
cnt[0] = 1
for i in range(n):
v ^= (1 << int(s[i]))
print(v)
ans += cnt[v]
cnt[v] += 1
print(ans)
