记录我的DP训练
D. Different Arrays
题意
给定一个长度为n的数组,必须进行$n ― 2$次操作,对$[2, n 一1]$范围内的数按顺序进行一次操作,一次操作为让左边和右边的两个数一个加上$a_i$一个减去$a_i$; ($a_i$指的是当前值),求操作后可能获得的数组的数量。
$$0≤a_i≤300, 1≤n ≤300$$
思路
看典哥题解写的…一开始还以为py用二维会炸(事实上也在炸的边缘),后来发现是自己太相信py的高精度了,被狠狠教育了
如果把结果放在最后才%MOD,可能会TLE或MLE
dp,看值域考虑dp,所有数最终能够变成的值域是$[-300 * 300, 300 * 300]$
二维版本
$f[i][j]$ 表示前$i$个数中,最终凑成的值$j$的方案数
每次先循环位置,再枚举当前位置最终变成的数
转移方程:
$$f[i + 1][a[i + 1] + j] += f[i][j]$$
$$f[i + 1][a[i + 1] - j] += f[i][j]$$
坑点:如果j = 0的话就只需要转移一次,要特判一下
一维版本
其实思路一样,不过是类似滚动数组,每遍历到一个$a_i$的新位置,用一个新数组存,然后覆盖老数组,就可以去掉$i$的维度。这样写居然不会MLE我也觉得很神奇
代码
def solve():
N = 310
n = int(input())
a = list(map(int, input().split()))
# f[i][j] = 前i个数中,最终变成的数为j 的方案数
f = [[0] * 90250 * 2 for _ in range(N)]
p = 90000
# 初始化,最开始只有位置2,值域也只能到a[2]
f[1][a[1] + p] = 1
for i in range(1, n - 1):
# 对于每个a_i,试探所有可能值(若在a_i前面的值使f[i][j]不为空,说明前i个数能够到达j这个值)
for j in range(-p + 300, p - 300 + 1):
if f[i][j + p] != 0 and j != 0:
f[i + 1][a[i + 1] - j + p] += f[i][j + p]
f[i + 1][a[i + 1] - j + p] %= 998244353
f[i + 1][a[i + 1] + j + p] += f[i][j + p]
f[i + 1][a[i + 1] + j + p] %= 998244353
elif f[i][j + p] != 0:
f[i + 1][a[i + 1] + p] += f[i][j + p]
f[i + 1][a[i + 1] + p] %= 998244353
ans = 0
for i in range(-p, p):
ans += f[n - 1][i + p]
ans %= 998244353
print(ans)
# 一维版本
def solve2():
n = int(input())
a = list(map(int, input().split()))
MOD = 998244353
p = 90005
ans = [0] * (2 * p + 500)
ans[a[1] + p] = 1
for i in range(n - 2):
dp = [0] * (2 * p + 500)
for j in range(-p, p + 1):
if ans[j + p] and j != 0:
dp[a[i + 2] + j + p] += ans[j + p]
dp[a[i + 2] + j + p] %= MOD
dp[a[i + 2] - j + p] += ans[j + p]
dp[a[i + 2] - j + p] %= MOD
elif ans[j + p]:
dp[a[i + 2] + p] += ans[j + p]
dp[a[i + 2] + p] %= MOD
ans = dp
print(sum(ans) % MOD)
这题的教训就是一定记得计算需要的数组长度(济南的签到好像也是这样栽了半天),和ans不要留到最后才模
C. Count Binary Strings
题意
给定一个01串,给定每一个区间范围内的限制。其中 g[i][j]表示对于区间[i, j]的限制。若g[i][j] = 1,说明这个区间内只能出现一种数;若g[i][j] = 2,说明这个区间内必须同时出现两种数;若g[i][j] =0,说明这个区间没有限制。求合法01串的数量。
思路
DP,观察发现若为合法01串,对于指定的右端点r,一定有:$a[1][r], a[2][r]…a[r][r]$呈现$2222…111..1$的特征。因为从后往前考虑,如果r - 1的位置与r的位置相同,则$a[r - 1][r] = 1$,否则为2。而一旦有某个位置为2了,这个位置往前的所有位置都会是2。
令$dp[i][j]$表示在前i个位置中,分界点为$j$的方案数(即,$j$以前为$2$,$j$及以后为$1$),答案为在位置$n$时的所有分界线位置方案之和,即 $$\sum_{i = 1}^{n}dp[n][i]$$
转移:从$dp[i][j]$开始,如果向后摆放的是和上一位相同的数,则j不变,转移到$dp[i + 1][j]$。若向后摆放的是和上一位不同的数,则$j$直接跳到$i + 1$,转移到了$dp[i + 1][i + 1]$。转移方程:
$dp[i + 1][j] += dp[i][j]$
$dp[i + 1][i + 1] += dp[i][j]$
注意这题还需要一个判断合法条件的操作,因为如果在$[1,j - 1]$区间有不该出现的$1$或在$[j, n]$区间有不该出现的$2$,则说明$j$在这个位置分割的方案是不可达到的,需要将该位置的$dp[i][j]$置$0$。
代码
def solve():
n = int(input())
a = [[0]]
dp = [[0] * (n + 2) for _ in range(n + 2)]
MOD = 998244353
for i in range(1, n + 1):
a.append([0] * i + list(map(int, input().split())))
dp[1][1] = 2 # 表示第一个位置可以为1可以为0
# l是分界点的坐标,在遍历前r个时,枚举分界点坐标
for r in range(1, n + 1):
for l in range(1, r + 1):
flag = 0
for k in range(1, l):
if a[k][r] == 1:
flag = 1
for k in range(l, r + 1):
# print(k, r)
if a[k][r] == 2:
flag = 1
if flag: dp[r][l] = 0 # 说明此处不合法,不满足22221111...
# print(r + 1, l)
dp[r + 1][l] = (dp[r + 1][l] + dp[r][l]) % MOD
dp[r + 1][r + 1] = (dp[r + 1][r + 1] + dp[r][l]) % MOD
ans = 0
for i in range(1, n + 1):
ans = (ans + dp[n][i]) % MOD
print(ans)
石子合并
题意
设有 $N(N \le 300)$ 堆石子排成一排,其编号为 $1,2,3,\cdots,N$。每堆石子有一定的质量 $m_i(m_i \le 1000)$。现在要将这 $N$ 堆石子合并成为一堆。每次只能合并相邻的两堆,合并的代价为这两堆石子的质量之和,合并后与这两堆石子相邻的石子将和新堆相邻。合并时由于选择的顺序不同,合并的总代价也不相同。试找出一种合理的方法,使总的代价最小,并输出最小代价。
思路
区间DP,学了一手区间DP的常见套路。详见代码
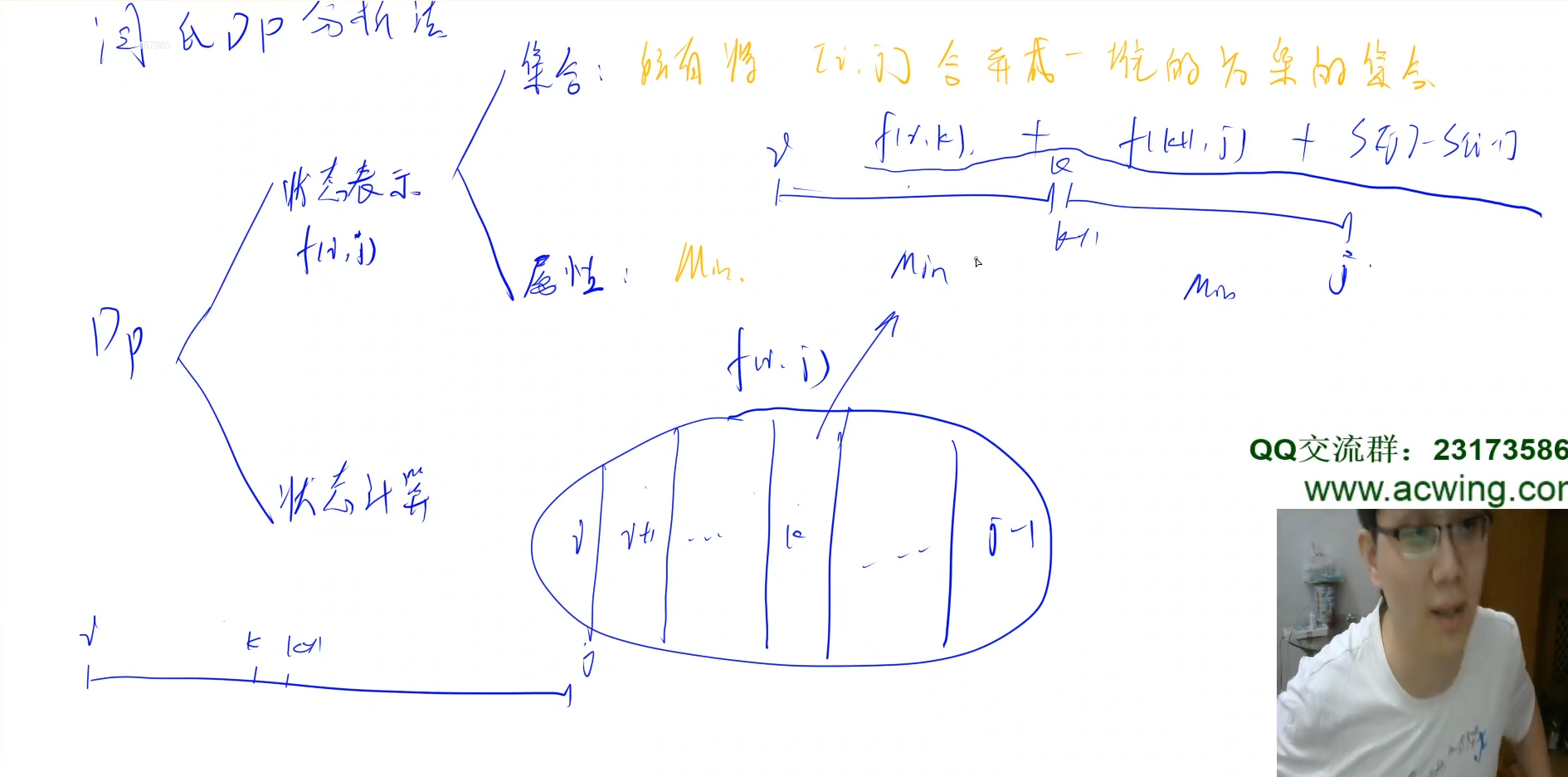
代码
def solve():
n = int(input())
a = [0] + list(map(int, input().split()))
s = [0] * (n + 1)
dp = [[0] * 305 for _ in range(305)]
for i in range(n):
s[i + 1] = s[i] + a[i + 1]
# 区间DP模板
for l in range(2, n + 1): # 先枚举区间长度[2, n]
for i in range(1, n): # 再枚举左端点
if i + l - 1 > n:
break
j = i + l - 1
dp[i][j] = 11451411
for k in range(i, j): # 最后在所枚举的区间中枚举分割点并更新答案
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + s[j] - s[i - 1])
print(dp[1][n])
C. Unstable String
题意
给一个字符串,其含有$0,1,?$. 其中,$?$可以看成$1$,也可以看成$0$。如果一个字符串可以是0和1交替出现的,就称这个字符串是$beautiful$。问现在这个字符串有多少$beautiful$的子串?
例如,
字符串$1,10$是beautiful的;
字符串$1???1$也是beautiful的,因为通过问号可以转化为10101;
但字符串$1???1$不是beautiful的,因为通过问号不管怎么变,都不可能使得01交替出现。
思路
最开始拿到手感觉很容易想到用奇偶去做,但是想不出来,找题解用dp做了
由于需要统计子串的数量,考虑统计每一位的贡献去做。
今天稍微又理解了一下贡献的概念,比如长度为$1$有$1$个子串,增加到$2$时新增了$dp[i] + 1 = 2$条子串,那长度为$2$的字符串一共就有$dp[1] + dp[2] = 3$ 条子串($dp[i]$代表新增到第$i$个时对答案的贡献)
用$dp[i][0]$和$dp[i][1]$分别表示以第$i$个数结尾,$s[i]$选$0$和选$1$的集合。属性是:新增摆放$s[i]$后,新增的合法子串数目(也即对答案的贡献)
转移分两种情况:
1、如果$a[i] = ?$,则$dp[i - 1]$的两种情况都能转移
$$dp[i][1] = dp[i - 1][0] + 1$$
$$dp[i][0] = dp[i - 1][1] + 1$$
2、如果为0或者1,则只转移一种,以 $1$ 为例,上一项为 $1$ 这一项为 $0$ 的构造是不可能的,因此,令当前项为0的构造方案也就不存在了,要重新置零开始。
$$dp[i][1] = dp[i - 1][0] + 1$$
$$dp[i][0] = 0$$
注意每次转移时需要取一个$max(dp[i][1], dp[i][0])$加在$ans$上。
代码
def solve():
s = '.' + input()
n = len(s)
dp = [[0] * 2 for _ in range(n + 1)]
dp[1][0] = 1 if s[1] != '1' else 0
dp[1][1] = 1 if s[1] != '0' else 0
# print(s[1], dp[1][0])
ans = max(dp[1][0], dp[1][1])
for i in range(2, n):
if s[i] == '?':
dp[i][0] = dp[i - 1][1] + 1
dp[i][1] = dp[i - 1][0] + 1
elif s[i] == '0':
dp[i][0] = dp[i - 1][1] + 1
elif s[i] == '1':
dp[i][1] = dp[i - 1][0] + 1
ans += max(dp[i][1], dp[i][0])
# print(dp)
print(ans)
C. Palindrome Basis
题意
给定一个数 $n(n \leq 4 * 10 ^ 4)$,问 $n$ 可以由多少种回文数的相加表示。
思路
预处理出所有回文数(大约不到500个)然后跑一个完全背包。
那么问题来了,怎么看出的是跑一个完全背包的呢。
令$dp[k][m]$表示仅使用前$m$个回文数来划分数字$k$的方法数。
观察得:$dp[k][m] = dp[k][m - 1] + dp[k - p_m][m]$, 其中$p_m$为第$m$个回文数。状态转移方程的意思是在$m - 1$时选了第$m$个回文数,那么就加上方案数。
可用滚动数组的思想将方程压缩到一维。
代码
def check(n):
temp = n
res = 0
while n:
res = res * 10 + n % 10
n //= 10
return res == temp
def init():
MOD = 10**9 + 7
for i in range(1, int(4e4) + 1):
if check(i):
v.append(i)
# print(v)
f[0] = 1
for x in v:
for i in range(0, int(4e4) + 1):
f[i + x] += f[i]
f[i + x] %= MOD
def solve():
x = int(input())
print(f[x])
if __name__ == "__main__":
v = []
f = [0] * 10 ** 6
init()
for test_case in range(1, int(input()) + 1):
solve()
