开新坑，先贴一下打的情况还算是有进步吧？第一场的时候还没报名，之后要找机会vp一场

从后往前补

2023牛客寒假算法基础集训营6

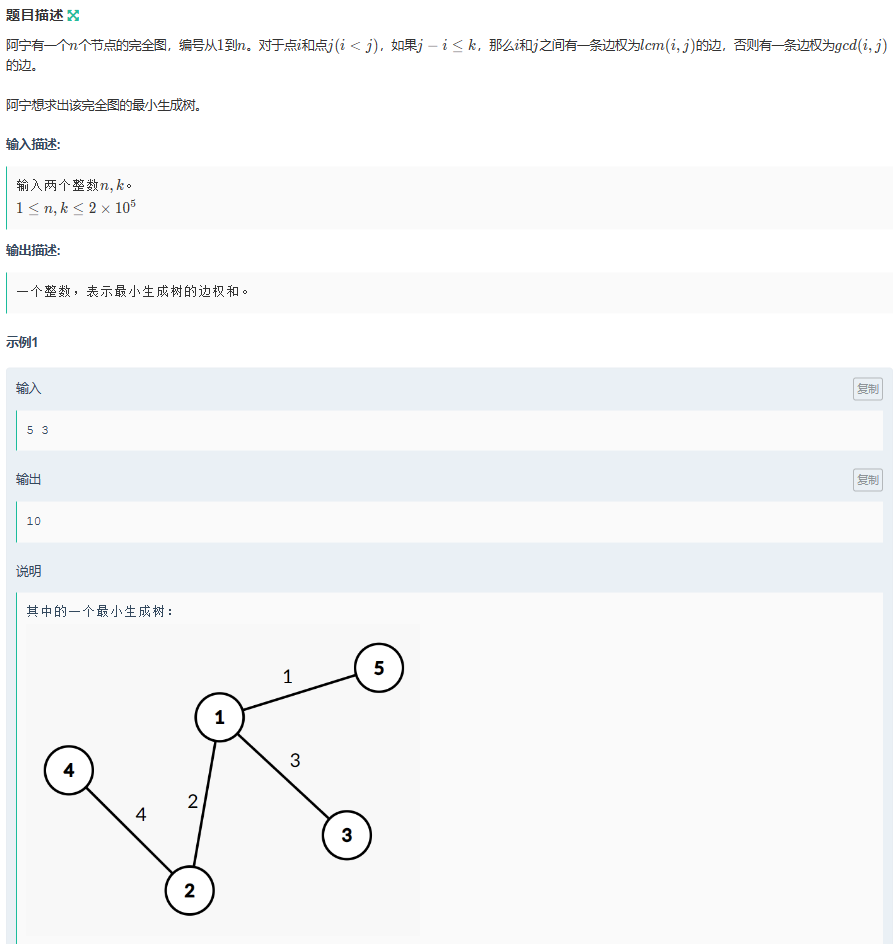
E 阿宁的生成树

题意

分析

实际上算是个脑筋急转弯，只要了解生成树的概念再想到一个小trick即可

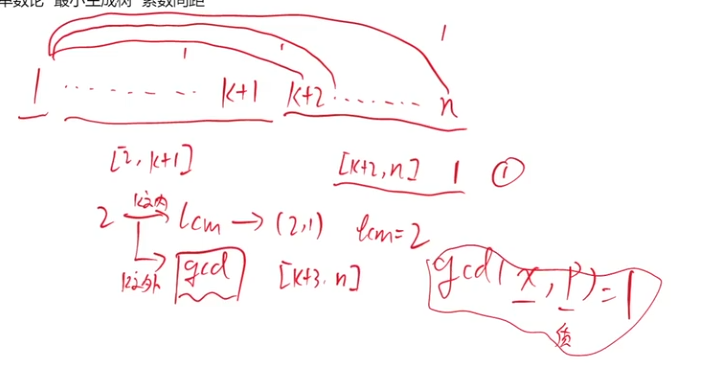
由于素数间的间距最大也就100左右，所以暴力枚举找素数是完全可行的来使$gcd(i, j) == 1$是完全可行的

连线策略：

代码

def solvee():
    n, k = map(int, input().split())
    ans = max(0, n - k - 1)
    for i in range(2, min(n, k + 1) + 1):
        temp = 1 << 31
        for j in range(k + 1 + i, n + 1):
            if math.gcd(i, j) == 1:
                temp = 1
                break
            temp = min(math.gcd(i, j), temp)
        mi = min(temp, i)
        # print(mi)
        ans += mi
    print(ans)

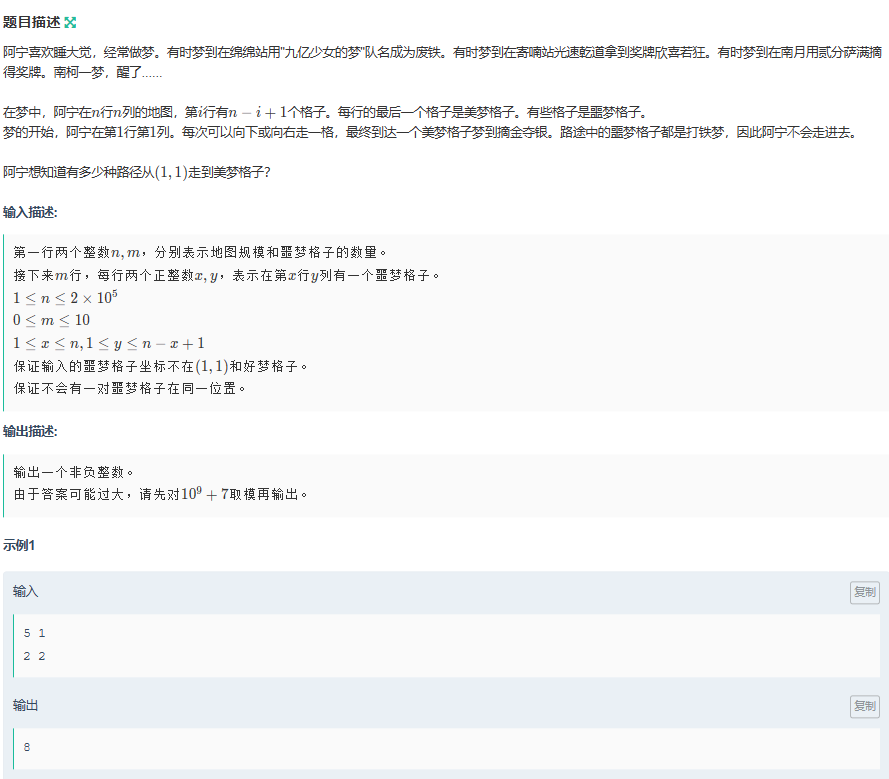
L 阿宁睡大觉

题意

思路

容斥原理 + 逆元求组合数取模 + dp

半理解半抄代码补完的…还是有点难理解，有时间一定要自己完整地写一遍

代码

这份代码的组合数取模板子似乎有点慢，跑了1600ms

def solvel():
    N = 2 * 10 ** 5 + 5
    MOD = 10 ** 9 + 7
    pow2 = [0] * (N + 1)
    b = [(0, 0) for _ in range(N)]
    fact = [0] * N
    infact = [0] * N
    fact[0] = 1
    infact[0] = 1
    for i in range(1, N):
        fact[i] = fact[i - 1] * i % MOD
        infact[i] = infact[i - 1] * pow(i, MOD - 2, MOD) % MOD
 
    def C(a, b, MOD):
        return fact[a] * infact[b] * infact[a - b] % MOD
    n, m = map(int, input().split())
    a = []
    for _ in range(m):
        x, y = map(int, input().split())
        a.append((x, y))
 
    pow2[0] = 1
    for i in range(1, n + 1):
        pow2[i] = pow2[i - 1] * 2 % MOD
 
    # 没有噩梦格子的总方案数
    ans = pow2[n - 1]
    for i in range(1, 1 << m):
        # 状压枚举
        t = 0
        t += 1
        # 先放入起点
        b[t] = (1, 1)
 
        # 格子为奇数时ok=1，偶数为-1（容斥原理）
        ok = 1
        for j in range(m):
            if i >> j & 1:
                t += 1
                b[t] = a[j]
                ok *= -1
 
        # 对x进行排序来一次判断是否会出现左下右上的情况
        b[1:t + 1] = sorted(b[1:t + 1])
 
        # 最后一个格子到终点的路径数
        temp = pow2[n - 1 - (b[t][0] + b[t][1] - 2)]
        for j in range(2, t + 1):
            if b[j - 1][0] <= b[j][0] and b[j - 1][1] <= b[j][1]:
                x = b[j][0] - b[j - 1][0] + 1
                y = b[j][1] - b[j - 1][1] + 1
                # 乘法原理，将路径数乘起来
                temp = temp * C(x + y - 2, x - 1, MOD) % MOD
            else:
                temp = 0
                break
        ans = (ans + ok * temp) % MOD
    ans = (ans + MOD) % MOD
    print(ans)

这份比较快，只跑了400ms

def solvel():
    N = 2 * 10 ** 5 + 5
    MOD = 10 ** 9 + 7
    inv = [0] * N; fac = inv.copy(); facinv = inv.copy(); pow2 = inv.copy()
    b = [(0, 0) for _ in range(N)]
    def C(n, m):
        return fac[n] * facinv[m] % MOD * facinv[n - m] % MOD
 
    n, m = map(int, input().split())
    a = []
    for _ in range(m):
        x, y = map(int, input().split())
        a.append((x, y))
 
    # 线性预处理组合数
    inv[1] = fac[0] = fac[1] = facinv[0] = facinv[1] = 1
    for i in range(2, N):
        inv[i] = (MOD - MOD // i) * inv[MOD % i] % MOD
        fac[i] = fac[i - 1] * i % MOD
        facinv[i] = facinv[i - 1] * inv[i] % MOD
 
    pow2[0] = 1
    for i in range(1, n + 1):
        pow2[i] = pow2[i - 1] * 2 % MOD
 
    # 没有噩梦格子的总方案数
    ans = pow2[n - 1]
    for i in range(1, 1 << m):
        # 状压枚举
        t = 0
        t += 1
        # 先放入起点
        b[t] = (1, 1)
 
        # 格子为奇数时ok=1，偶数为-1（容斥原理）
        ok = 1
        for j in range(m):
            if i >> j & 1:
                t += 1
                b[t] = a[j]
                ok *= -1
 
        # 对x进行排序来一次判断是否会出现左下右上的情况
        b[1:t + 1] = sorted(b[1:t + 1])
 
        # 最后一个格子到终点的路径数
        temp = pow2[n - 1 - (b[t][0] + b[t][1] - 2)]
        for j in range(2, t + 1):
            if b[j - 1][0] <= b[j][0] and b[j - 1][1] <= b[j][1]:
                x = b[j][0] - b[j - 1][0] + 1
                y = b[j][1] - b[j - 1][1] + 1
                # 乘法原理，将路径数乘起来
                temp = temp * C(x + y - 2, x - 1) % MOD
            else:
                temp = 0
                break
        ans = (ans + ok * temp) % MOD
    ans = (ans + MOD) % MOD
    print(ans)

2023牛客寒假算法基础集训营5

C 小沙の不懂

题目描述

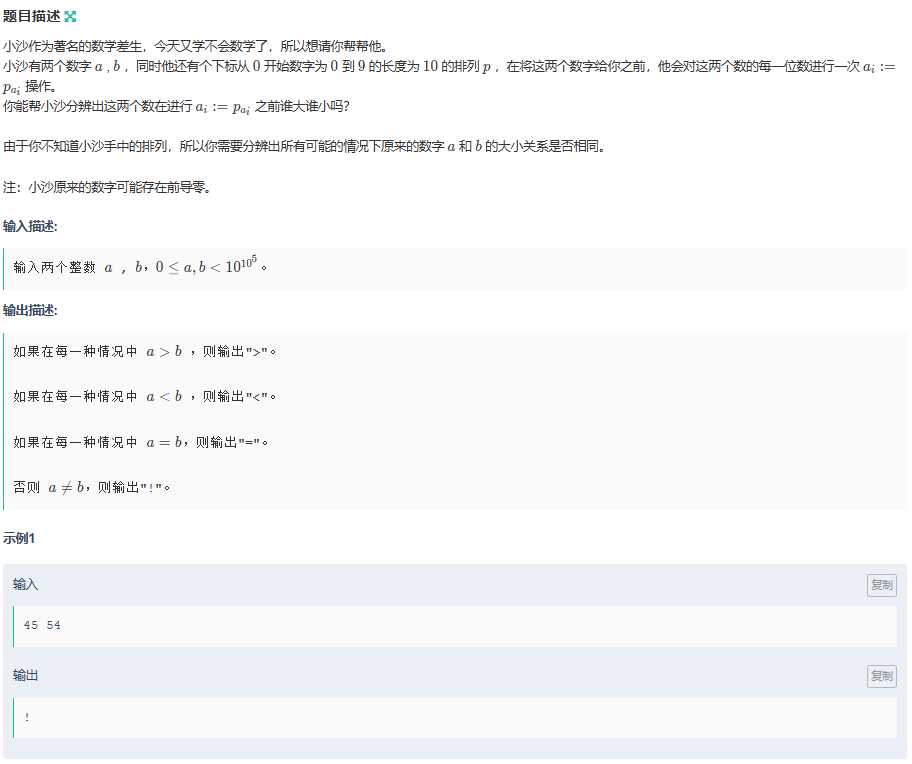
沙姐姐的题面太难顶了，用炸鸡块哥哥的话翻译下题意：

$p$相当于是一个映射，将原来$a, b$中的数字映射成现在的输入，题目问你是否不管这个映射$p$怎么变，是否能确定原来$a, b$之间的关系，如果能就输出大小等于，不能则输出！

思路

在打这场的时候就看群友说这题十分的阅读理解，~~gkjj差这题就ak。~~于是果断选择跳过去做其他题

直接贴结论吧

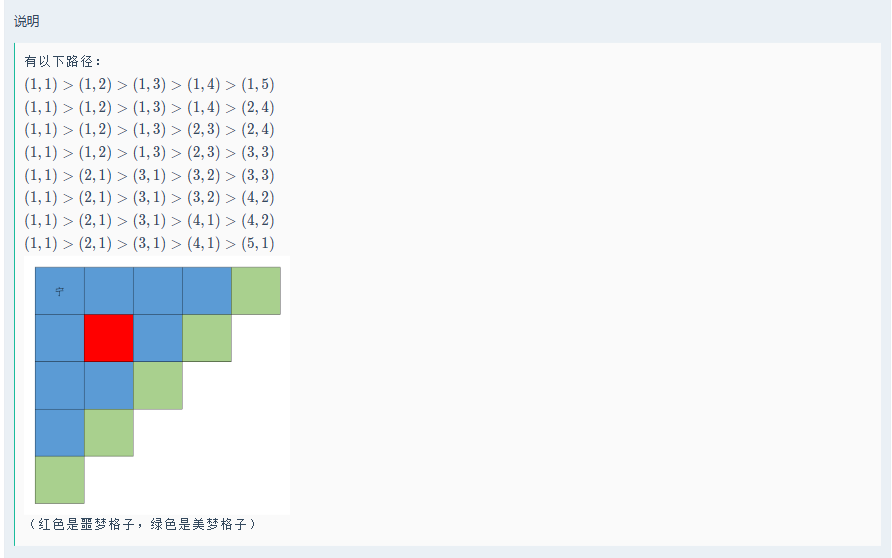
长度不一样的时候，如果要让长的不一定大于短的，只有一种可能。贪心地想，肯定是要将长的那个多长的一截给去掉，即变0，如果不能去掉则长的一定大于小的。

一长一短的情况只有两种情况：长的大于小的或不能确定，不能确定的情况比较好找，有两种：

剩下的$a, b$完全相同。此时由于前面截掉部分的不确定性，有大于和等于两种可能。
从前往后找，若找到一个不同，如果不同且$b[i]$不等于之前截掉部分的数（即不能变0），说明长的失去了最后的一定大于短的机会，也是不确定。

剩下的情况，长的一定总是大于短的

代码

def solvec():
    a, b = input().split()
    if a == b:
        print("=")
        return
    if len(a) == len(b):
        print("!")
        return
    res = ">"

    if len(a) < len(b):
        a, b = b, a
        res = "<"

    n = len(a)
    m = len(b)
    ok = a[0]
    for i in range(n - m):
        if a[i] != ok:
            print(res)
            return

    a = a[n - m:]
    if a == b:
        print("!")
        return 
    for i in range(m):
        if a[i] != b[i]:
            if b[i] != ok:
                print("!")
                return
            break  # 这个位置一定记得break，只比较一次
    print(res)

F 小沙的串串

题意

思路

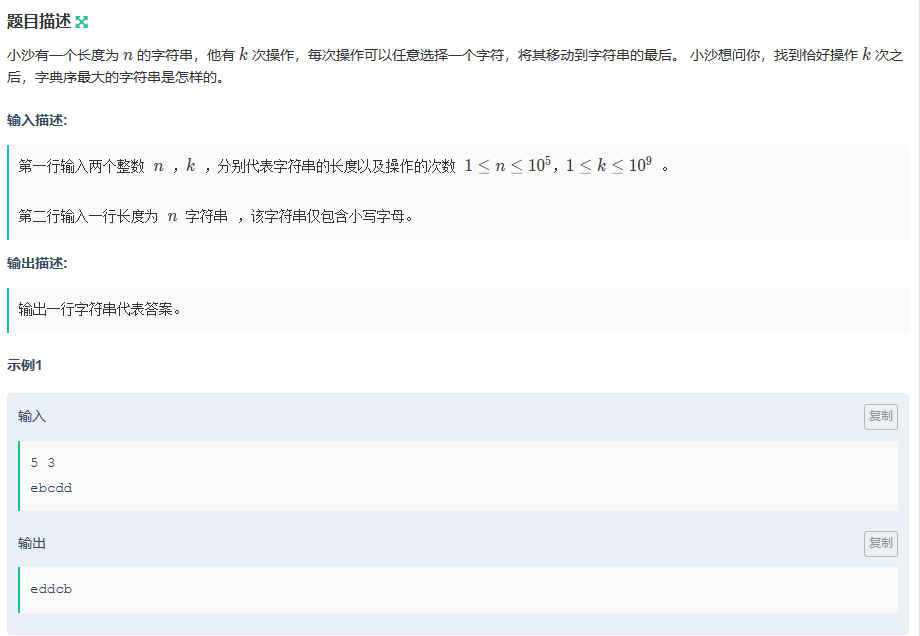
这题赛时过的人很少，最后1h才逼近100，但群友说是典中典。~~看来确实做少了~~

大体的思路就是用单调栈模拟，由于每次操作可以使得更大的数字往前移动，所以可以采用单调栈来维护一个单调递减的数字串。单调栈里面的一定是一个单调递减的字符串，并且栈底是操作后字符串的首位（能达到的最大值）

关键点来了，如果对整个串维护完之后，如果存在多余的操作没有使用，则可以选择最后几个最小的数字将其放在后面，使得前面曾被移动的到后面的数字更加靠前。

随后将所有被移动后的字符排序之后，接在最后面即可，因为我们的操作其实是不分先后顺序的，没有规定一定要挨着删。因此我们可以先将需要删除的最大的字符进行删除，使得最后他尽可能的靠前。来达到排序后的效果。

代码

def solvef():
    n, k = map(int, input().split())
    s = input()
    ans = deque()
    res = ""
    for c in s:
        while k and len(ans) > 0 and ans[-1] < c:
            k -= 1
            res += ans.pop()
        ans.append(c)

    while k and len(ans) > 0:
        k -= 1
        res += ans.pop()
    res = sorted(res, reverse=True)
    temp = [c for c in ans]
    temp.extend(res)
    print(*temp, sep="")

2023牛客寒假基础算法训练营

6场还算不错的比赛